|
Why Un DIY ING? Just because the laser diode is a ready-made commercial grade
device and DIY technologies can only be applied to create a power supply or a
nice looking housing. Or, maybe, for the focusing optics (if it is really
needed there). In fiction the word "undying" means scary creatures with hell
nature. Well, powerfull laser diodes don't frighten anybody, the feeling they
give rise to, is closer to envy. However for the strict developer of homemade
lasers it may be kinda shameful to fall to use of some ready made commercial
laser.
Anyways, the text devoted to usage of laser diodes has finally appeared at
this site. This is not a guide. It looks more like a public domain textbook.
And for this reason it is placed in "technologies" department.
I need to warn: this text is intended for the "saber-builders" - those ones,
who thinks, that a thing may be called as "laser" only when it is able to burn
and cut with its ray of light. Thus the problems of low power laser diodes
(weaker than 1 Wt) are not discussed here. The specific problems, like width
of spectrum or wavelength stability are omitted too.
Contents
- POWER SUPPLIES FOR LASER DIODES
- SIMPLE ANALOG CURRENT REGULATORS
Simple circuits of analog constant current sources are presented. These
circuits are best for driving of laser diodes. The circuits can be
built successfully by a technician of amateur level.
- PULSED CIRCUITS
Schematic of pulsed mode power supplies are (to be) presented. These
are SMPS current regulators, voltage regulators and hybrid circuits.
WARNING: to build and debug these circuits one may need the abilities
of specialist in electronics of higher than average level.
- LASER DIODES AND THEIR PARAMETERS
The meanings of the main parameters of laser diodes are explained. There
is also a list of recommendations for proper choice of laser diode for
buying.
- THE OPTICS
Basic knowledge of geometrical optics is reminded. The meaning of main
terms is described. The typical optical schemes of most importance for
lasers are discussed. Simple formulas for calculations are provided.
There are also examples of calculations.
- METHODS OF POWER INCREASEMENT BY ADDING MORE LASER BEAMS TOGETHER
- GEOMETRICAL ADDITION
There described how to make a beam combining system of a popular "knife-edge" type without using professional equipment. An example
is given of gathering the light from four laser diodes into practically
single beam having the total power of 16 Wt.
- POLARIZATION ADDITION
A method of combining two laser beams with different polarization into
one beam is described.
- SPECTRAL (COLOR) ADDITION
A method of combining many laser beams with different colors into one
beam is described.
It appears that the title of this text tunes to the mood of mystics and
religion. So here are some dogmata being in use among the people having deal
with laser diodes. How to apprehend them and how to treat - one can read this
inside the text.
Power supplies for laser diodes
↑
On the power supply: It is relatively wide known already that one must feed
the laser diodes using so called "constant current source" and not by a voltage
regulator. The simplest are the analogue regulators. Here is a pair of good
circuits.
Circuit N1
↑
The circuit is based upon one chip voltage regulator being connected as a
constant current source:
____________
/ O \
| |
--------------
| KPEH22A |
| LT1083-CT |
| |
|Adj Out In |
-+----+-----+-
| | |
| +--+ |
| | | SW1 6 Amp
R2..R5 +-/\/\/-+ | /
1.0 Ohm | | +---------+----+ +------+
each +-/\/\/-+ | | |
| | | | 2 x 18650 |
+-/\/\/-+ | | Li-Ion |
| | | | cells -----
5W +----->>--+-----------+-------+-/\/\/-+ | | ===
808 nm | | | C1 | C2 | R6 -----
_+_ / R1 | >400uF | >400 uF / 10 kOhm ===
Laser \ / \ 10 kOhm --- LOW ESR --- \ |
Diode -+- / --- --- / |
| | | | | |
+----->>--+-----------+------------------+---------+--------------+


Resistors R1 and R6 are only to discharge electrolytic caps C1 and C2 safely.
The voltage here is always not higher than 10 volt, so the word "safely" does
not mean any danger to Your health or life. On the contrary the charge of C1
and C2 is VERY dangerous for the life of the laser diode. In case of any random
contact it can easily kill the precious device.
C2 capacitor serves for prevention of SW1 switch ringing.
C1 capacitor is of the very importance here. Calculations in LTSpice and
modeling on real circuits does show that there exist a positive and non-zero
value of the capacity of this capacitor, below which the circuit refuses to
operate - it produces an over-regulating overshot current and kills the diode.
This threshold capacity is individual and depends to the voltage regulator
chip parameters as well as to the current setting. For most chips like LT1083
it is about 100-200 mcf. For LM317's this value is lower. So if we chose it
to be C1>400mcf we should have enough of safety margin.
Resistors R2..R5 are current measuring/current setting ones. Generally the
principle of operation is just to force the on-chip voltage regulator to set
the constant voltage across the fixed resistor. Since the voltage is constant
and the resistance is constant, the Ohm's law will unavoidably set the current
to be constant too. The resistor is composed from many ones. There are three
good reasons to do so:
- They dissipate high power;
- The errors of their resistance will partially compensate each other;
- By varying of the number of soldered resistors one can vary the value of the
current, being produced by the circuit. (And thus to set the power of the
laser.)
Avoid to use a potentiometer here! It is a proven way to kill the laser diode.
Avoid switches too. One can vary the number of the resistors by soldering only.
In the worst case You can use computer jumpers. But only if You are sure that
they are reliable enough.
Bonuses of the circuit:
This circuit is VERY simple and uses VERY affordable parts. Along with this
it has a high precision and many of internal protections of any kind: from
shortcircuit, from overheat, from overvoltage of the power supply and so on...
Maluses of the circuit:
Despite the comprehensive set of protections the circuit is NOT protected
from the reverse polarity. So be extremely attentive when installing the
batteries.
Another issue is that this circuit hates a bad connection between it and the
laser diode. Indeed, when the connection is bad the constant current generator
tries to rise the current and charges the C1 cap. And when the connection
recovers, all the charge from C1 flows through the diode and kills it.
This drawback is more or less the property of any constant current type
regulator. Use reliable wires and soldering. One should never try any kind of "poking" of the leads of the laser.
The circuit is brakish enough. The typical rise and off time is well above one
millisecond, and it is determined by charging the C1 and C2 caps. However
remember that those caps are chosen exactly due to the properties of the chip
itself. So we can say that the circuit is slow due to the fact that those
voltage regulators are too slow themselves.
Another issue is that the circuit behaves badly under the dynamic changes of
load. It is very expectable - there is no limits for the current to flow
between the large capacity C1 and the laser diode. With powerful gallium
arsenide diodes (red and infrared ones) there is nothing bad here, but with
gallium nitride ones (blue and green) it may cause failures. The last ones
behave like they have an area of negative differential resistance, like tunnel
diodes.
One should also keep in mind that some of the on-chip voltage regulators
are fake ones. When buying those LT1083, LM196, LM338 etc one can easily
face something very wrong under the good looking outfit. So ALWAYS CHECK
THE CORRECT OPERATION OF THE NEWLY ASSEMBLED CIRCUIT BEFORE CONNECTING
LASER DIODE TO IT!
Tho check it out it is better to load it by different resistors and to look
how the current depends to the load. Hint: if the circuit works correctly the
current should remain almost constant with any reasonable variations of load
(say between zero/shortcircuit and one Ohm).
If one has an oscilloscope it is very desirable to check the rise and fall
curves occurring during turning the circuit on and off.
Generally the impression is very positive from this circuit.
For better safety one should add a diode between the battery and the circuit -
it would protect from the reverse polarity, and add a small resistor in series
with the laser diode (like 0.5-1 Ohm) - it will make it more stable under the
dynamic changes of load. However these improvements cause high overhead in the
required size of the battery. Consider 1 additional volt across the protective
diode and one or two volts across the stabilizing resistor.
The efficiency of the circuit grows with rising the voltage drop on the diode.
So using this circuit to feed a blue diode (4.3 V) or to feed two IR diodes
in series (4.8 V) one can expect the efficiency as high as 50%.
This circuit has:
- Powered two portable 5W lasers for reasonably long time without a fail;
- Burned out one red diode from DVD drive - a try to control current by
a variable resistor;
- Burned out one blue diode. It is when it was found out that with this circuit
and the blue ones, one should not exceed a half of the current rating of the
diode being used.
 Return to contents Return to contents
Circuit N2
↑
Two transistors as constant current generator.
There are several variations based on the same idea:
NPN + MOSFET:
/
+--+ +---|>|-------+---------------------+
| SW1 10A10 | |
| | |
| \ R1 |
| / 100 Ohm irf3205 |
| \ |-+Drain
| / Gate||
| |__________________J|-+
| | | |-+Source
| |Collector | |
| 2 cells \ | |
| Li-Ion 2n2222 \|Base | |
| 18650 /|----------)-------+
| / | |
----- |Emitter R2 \ \ R3
=== | 10k / / 0.14 Ohm
| | \ \
| | / /
----- | | |
=== +-------------+-------+
| |
| +-----+------+ 5W
| | C1 | | 808 nm
| R4 \ 10u| | Laser
| 10k / --- _+_
| \ --- \ /
| / | -+-
| | | |
+----------------------------+-----+------+
NPN + NPN:
/
+---+ +---|>|-------+---------------------+
| SW1 10A10 | |
| \ TIP41C |
| / R1 2N3055 |
| \ 100 Ohm kt819 |
| / |
| | |/ Collector
| +-------------+-----|
| | | Base|\
| |Collector | |Emitter
| 2 cells \ | |
| Li-Ion 2n2222 \|Base | |
| 18650 |----------)-------+
| /| | |
----- /Emitter R2 \ \ R3
=== | 10k / /
| | \ \
| | / /
----- | | |
=== +-------------+-------+
| |
| +-----+------+
| | C1 | |
| R4 \ 10u| | Laser
| 10k / --- _+_
| \ --- \ /
| / | -+-
| | | |
+----------------------------+-----+------+
One could imagine a MOSFET+MOSFET here, but due to (comparatively) high voltage
needed to turn a MOSFET on the voltage drop over the current-measuring resistor
R3 would be 2.5-3 volts even for the so called "logical driven" MOSFETs. And
it is quite an overhead.
In the NPN+NPN variant the circuit was tested with a 5W 808 nm diode, The kt819
transistor appeared to be tough enough, so three channels in parallel were used.
A "heavy-caliber" laser pointer worked flawlessly until the attempt to use
a commercial constant current driver there. That diode was burned out, but the
described driver has nothing to do with that.
Another variant was specially intended for use with batteries:
/
+--+ +--+--|>|-----+---------------------+-----+
| SW1 | 10A10 | | |
| | + C3 | | 5W
| --- C1 / SW2 3.3n --- _+_ 808 nm
| --- >100uF + --- \ / laser
| | | | -+-
----- | \ | |
=== | / +-----+
|18650 | \ R1 |
|2 cells | / 100 Ohm irl540 |
|Li-Ion | | |-+Drain
----- | +------+ Gate||
=== | | |__________________J|-+
| | | | | |-+Source
| | | |Collector | |
| | | \ | |
| | | 2n2222 \|Base | |
| | | /|----------)-------+
| | | / | |
| | --- |Emitter R2 \ \ R3
| | --- C2 | 10k / / 0.14 Ohm
| | | 0.2 | \ \
| | | uF | / /
| | | | | |
+--------+---+------+-------------+-------+



In previous variants the diode was connected in series with the current
regulator. It is correct, since the constant current generator makes the
current to be constant in anything connected in series with it.
As one can see in the last scheme the diode is included into the drain
circuit of the mOSFET. This allows to avoid the subtraction of the voltage
drop on the diode from the total power supply voltage. So the full supply
voltage is available to control the gate of the MOSFET.
The drawback of this connection is that the laser diode is under a voltage
in relation to the common wire (to the ground wire). Sudden shortcircuit
to the ground - and the diode is dead. Nevertheless in battery powered
circuits the term "ground" is rather conditional one, and we can utilize
such a connection if not planning to feed the device from the mains.
If one uses a logic level MOSFET (like irl540 or irlr2905), if the laser
diode is red or infrared and if the reverse polarity protection diode is
excluded (shorted), the scheme becomes able to operate from a single Li-Ion
battery (3.7V). It is cheaper, occupies less size and also there is much
less of heat on the transistor. The price is however is the danger to kill
the diode by inserting the battery in reverse.
In all variants of the circuit there is a sense to compose the R3 resistor
from several discrete ones. The necessary value of the constant current can
be selected by soldering the necessary amount of the resistors. It is clear
that until the proper current value has been set, one should never connect
a real diode as the load. Use a 0.5-1 Ohm resistor there or a pair of
powerful rectifier diodes in series there.
C1 capacitor is the protection from the SW1 switch ringing. The ringing
of SW2 affects performance much less, because SW2 conducts only a small
current, limited by R1. Also the soft turning on (provided by slow
charging of C2 through R1) is the very mean to lessen the harmful influence
of the switch ringing.
THE MALUCE OF THE CIRCUIT is there is a lack of reference voltage. In
practice it means that any newly assembled circuit needs individual tuning
by variation of R3 value. There is no compensation of the temperature drift
also. Besides for the independent reasons You don't want to turn on this
driver when it is too cold (winter) or too hot. In the first case there is a
danger to kill the diode due to the humidity condensation. In the second case
there is a danger to kill the power MOSFET and/or the laser diode due to the
overheat, since the circuit has no means of the overheat protection.
THE BONUSES OF THE CIRCUIT are:
- The possibility to operate using a single Li-Ion battery (when using some
logic level MOSFET and without the reverse polarity protection diode);
- Excellent damping of transient current under the dynamic load variations
due to the absence of a large capacitor in parallel to the laser diode.


Usually this scheme leads to comparatively large size of driver. Mostly
it is due to the large heat-sink of the power MOSFET. If (as it often happens)
the efficiency is factor of no importance for You, and You are bothered only
by the MOSFET overheat, the circuit may be made much smaller just by moving
the heat dissipation place from the MOSFET to some resistor. Simply add a
resistor in series with Your laser diode. The exact value of the resistor
should be verified by trials and errors at some large sized model of the
circuit with a heavy heat-sink. This value depends on the voltage of Your
battery and the desired current. (For feeding powerfull diodes from a pair
of Li-Ion battery the necessary resistance is usually about 1 Ohm). The
added resistor reduces the voltage drop across the powerful MOSFET and hence
makes its life easier. On the other side, most resistors can operate safely
at temperatures of the order of ~200 degrees of Celcium, and thus do not
require any additional heat sink.
On the photos below an example of miniature two-transistor current regulator
is shown. It has additional resistor for the MOSFET relief. The driver is
intended for use inside a standard laser pointer housing.



Both circuits are simple enough and if there are no soldering errors they
begin to operate properly right after having been assembled. The only tuning
is to chose the correct value of the current measuring / current setting
resistor (R2-R5 in the circuit with on-chip voltage regulator and R3 in the
circuit based on two transistors). In order to do it, solder a dummy load
to the output terminals of the circuit (in place of the laser diode) and
adjust the value of the current setting resistor until the desired current
is obtained. In the simplest case one can use a resistor (0.5-1.0 Ohm rated)
as the dummy load.
The current through the load may be measured in several different ways:
- If a simple resistor is used as the load one can simply measure the voltage
drop on it using some multimeter, The value of the current can be readily
obtained by applying the Ohm's law.

- One may connect a multimeter in series with the load. The multimeter should
be switched to ammeter mode in this case. For these measurements I advise
to make an additional set of probes for the multimeters. The proper probes
should be short enough (not longer than 10 cm) and made of thick wire.

- One can attach an additional current-measuring resistor in series with
the load and measure the voltage drop on it. This method is especially useful
when measurements are made by an oscilloscope.

- And finally one can measure the voltage drop over the current setting
resistor. However two conditions are to be met here:
First: the value of the current setting resistor must be known precisely.
It is easy if the one is formed by a number of commercial resistors. And
it is almost impossible if You are using a piece of wire there and adjusting
the length of the wire until the necessary load current is obtained.
Second: the stay currents there are to be negligible in comparison with the
main load current.
The stray currents are: the ADJ lead current in the circuit
with on-chip voltage regulator or the base current of the control transistor
in the circuit based on two transistors. This is easy if the diode to be
used is powerful and the full load current has the value of several Amps,
and this is not so easy when trying to drive diodes of low or medium power.
Sometimes the two-transistors driver shows a tendency to oscillate at high
frequency (like ~30 MHz). Sometimes it takes place only in moments of switching
on/off. In other cases it can show permanent oscillations. In case of permanent
oscillations it is easy to diagnose them with a multimeter. If the circuit gives
too low current (in comparison with the expected value) and if there are no
soldering errors, it means the HF excitation. The temporary HF bursts during
switching on and of can only be seen using an oscilloscope.
If the HF excitation takes place one can try to jam it by including some
50 Ohm resistor between the base of the control transistor (2n2222) and the
point of signal taking from the current measuring resistor R3. One may also
use ferrite beads, since the main purpose of their design is to dampen the HF
oscillations. One can also try to replace the control transistor (2n2222) with
another one, having lower frequency border. The russian kt3102 works good
here. I am sorry, but due to the lack of testing, I can not recommend some
good transistor from the international nomenclature.
And finally the most correct and effective way to jam the RF oscillations is
to reorder the printed circuit board geometry.
When You have tuned the scheme, You need to check whether it really does
regulate the current or not. In order to do this measure the current several
times, each time attaching different resistor as a load. The current should
stay reasonably constant. (For the two-transistor circuit the changes of
current in range of 5-10% are acceptable.)
One need to keep in mind that both schemes require that the voltage drop
over the load should be less than the supply voltage minus the voltage drop
over the current-setting resistor and minus some additional voltage drop
of the regulator element (~1V for the on-chip regulator and bipolar transistors
and equal to the voltage drop over the open channel resistance for MOSFETs)
In other words You can not choose too high value of the load resistor.
On the contrary You can freely choose the value of the load resistor to be
as low as zero. Since the circuit regulates the current it wont affect much
its safety or performance. Nevertheless If You measure the current by the
voltage drop over the load resistor get ready to face huge measurement errors
id using too small resistance there.
If You have an oscilloscope (and if You are going to make some laser diode
drivers You definitely ought to get one) then BEFORE ATTACHING THE REAL LASER
DIODE TO THE OUTPUT OF THE SCHEME check the absence of current overshots when
switching the circuit on and off. For the two-transistor scheme it is good to
check for the absence of current overshots during dynamic load changes. To do
this make the dummy load using the next schematics:
o--------------------+-----+
| |
| +
| / SW
| +
| |
/ /
\R1 \ R2
/ /
| |
o----+---/\/\/---+---+-----+
| R3 |
^ ^
A B
Where R1 and R2 have the value of the order of the laser diode resistance at
its working mode. (For example for a five watt rated infrared diode:
R1 = R2 = 2.4V / 5A = 0.48 Ohm ). The R3 resistor should have its value as large
as R1/10...R1/5.
The oscilloscope's probe is to be connected in parallel to the R3 (points A and
B on the scheme). When turning the SW switch on and off there should be no
noticeable overshots and ringing.
Generally the powerful laser diodes are the devices heavily overstressed
in several parameters (Like the electrical and optical power density, electric
field tension and so on) so they die by every sneeze. And they cost damned high
and to loose one is a tragedy and funeral. So to use the laser diodes is less
science than a mysticism and religion. The science is based on observational
facts and argumentation. The religion is based on dogmata.
DOGMA THE FIRST - DOGMA OF LASER DIODE INFALLIBILITY.
It can be expressed as that: IF THE LASER DIODE HAS DIED ITS POWE SUPPLY IS
GUILTY.
There are other dogmata too, but lets stop here for a time.
It is considered that even the smallest surpass over the allowed limits,
even for the shortest time is strictly forbidden. For example a datasheet of
5 watt rated infrared diode says that the maximum current is 5 amps. One
should get is "YOU are not allowed to overshot it even by 1 mA even for 1 ns"
Moreover it is considered that the reverse polarity is strictly forbidden.
Even for 1 mV over 1 ns. It means You can kill the laser diode by Your
multimeter in an attempt to find its correct polarity. (In practice I don't
remember any case of killing a laser diode by a multimeter, but it is HERESY
to doubt in dogma)
Even worse that it is considered that one must never exceed the maximum
allowed output power. (Even by one milliwatt during one nanosecond). Why I say "worse"? Because in general the watt-ampere characteristic of the diode (in
other words its efficiency) depends at least to its temperature. And You
can easily exceed the top allowed power even when keeping the supply current
in the allowed limits. Just by using it outdoors in cold weather. It is
considered that a proper driver should contain an optical feedback to keep
the output power in its limits. For the further details I'd better send You
to Sam'S Laser FAQ, because we wont apply all those features here. Otherwise
our simple LD driver will blossom with hundreds of protections and thousands
of sensors, and it will grow a data center nearby to process the data from all
the censors and to elaborate a strategically weighted solution on its base.
Dogma of the diode infallibility leads to two things in our case:
| First: |
If Your don't want to shed the tears on the prematurely passed away
laser diodes (our precious), there is no such words as "forgot" or "was lazy" to You:
"Forgot to check the current"
"Forgot to check
for overshots"
"Too lazy to check, I've build a thousands of such
drivers, what can go wrong?" |
| Second: |
When You know that the smallest excess of parameters is strictly
forbidden, and when You know that any real device (including Your
driver) has some spread of parameters, the obvious conclusion is
that You must "derate" (or "downrate") the device. It means You
must provide a sufficient difference between the value of the
current You driver supplies and the value of the top allowed current.
That safety margin must be large enough to keep the current, power
and any other parameters in their safe limits in any case. (In case
of any variations of the supply voltage, of the ambient temperature,
etc.) |
Performing deratization, sorry, derating of the diode You are being between
two sides: on one hand You don't want to put too much power to avoid killing the
diode and on the other hand You don't want to pot too low power - or else
would not it be simpler to buy a 10 mW green pointer in the nearest stall?
It is understandable that if one does not exceed a half of the top allowed
current (e.g. 2.5 amps for that 5W rated infrared diode, having been used as
example many times above) it almost warrants the safety of the diode, but the
output power won't be acceptable.
Blessed the one, having a bunch of laser diodes, and having the opportunity
to kill a few of them to estimate the borders of the allowed. Others are usually
in lack of such possibilities.
Sometimes the manufacturer suggests the optimal (to his opinion) amount of
derating. For example Nichia NUBM08 diodes are strongly recommended to be fed
by a current not exceeding 3 amps. At the same time the table of absolute
maximum rating in its datasheet contains the value of 3.5 amps. Most other
manufacturers lack such a respect to the clients.
The real value of the current You decide to set depends:
- To Your assurance in the driver's reliability.
The lower is the precision of the current regulation, the larger safety
margin You will choose.
- To Your assurance in the laser diode reliability.
The diodes of top rated manufacturers (such as nLight, Osram) have a good
probability to operate flawlessly at the current of 95-99% of the top
allowed one. "Noname" diodes should be fed by the current that corresponds
to 60%-80% of the top allowed output power. (If You have no power meter -
set the current to 60%-80% of the top allowed current for this diode.)
- To Your prosperity.
Indeed if You can bear easily the death of a few laser diodes, You can
drive the diode to the maximal allowed current (or even higher) without
the excess of care. And for You it may be worth to burn out every other
laser diode only to boast the "most powerful laser pen in the world"
- And finally it depends to Your bravery/insolence.
If You feel being the gambler, I recommend to set the current to 110%-120% of its maximum allowed limit. In case of success You will become
the owner of the "most powerful in the world, etc, et..." In case of
fail - just consider it wasn't Your day.
In any case I would not recommend to exceed 150% of the maximum allowed
limit even to the most hardcore gamblers.
There exist another one interesting circuit for current regulation. It
has the name "current mirror":

Its principle of operation is that a transistor (either field one or bipolar
one), when being at linear part of its working characteristic, can itself work
as a source of current (means current regulator). One needs only to adjust a
bias on its base(gate). The required accuracy of this adjustment is high so
it cannot be made manually. The left part of the circuit is essentially the
authomated generator of this bias for the right part. Due to the base of the
left transistor is directly connected with its collector, the bias on the base
authomatically settles at the level, that provides the current, that flows in
the left part. This current can be set by R1 resistor. Note that this current
is not exactly equal to V1/R1, because the voltage drop over transistor Q2
can not be zero. In practice one could measure the collector current of Q2
(or measure voltage drop over R1) and adjust the R1 value so that the current
has the desired value.
After this the bias on the base of Q1 transistor becomes the same as it is
for Q2 transistor, and if the transistors are identical, their collector
current will be identical too: I(Rload)=I(R1) for any loads that obey Rload<R1.
They say that the right side of the circuit "reflects" the current of the left
side. This is the reason for the name "current mirror".
If things were limited only by that the circuit would be of zero importance
for laser diodes feeding. Indeed, who wants to waste, say three amps of current
in the left shoulder of the circuit, for only to get the same three amps in the
right shoulder? However the things aren't so bad in reality. Just try to
install a low power transistor into the setting shoulder of the circuit and
a high power one into the regulating shoulder. This approach works not only
with bipolar transistors, but with MOSFETs as well:


In this case it will appear that the current in the shoulder with the load is
higher than one in the shoulder with the current setting resistor. I.e. waste
of energy of the energy source became lower and the efficiency of the circuit
has grown up. One can say that it is a "curved current mirror".
Now about the shortcomings:
One can understand easily that if the voltage of feeding source becomes
higher the current in the current-setting shoulder will rise up. The current
in the forcefull shoulder will rise also. It does not mean the surge of current
regulation. It just means that the circuit is stabilized in relation to the
load, not in relation to the feeding source. On the contrary the previous
circuit of the responds
not only to load change but to feeding voltage change too.
However the fact that the circuit responds only to changes of load is not
very serious drawback. In stationary circuits one can easily provide regulation
of feeding voltage, while in portable things the voltage of batterries is
usually known well, and if the driver does not exceed the maximal allowed
current of laser diode with fresh batterries, there will be no excess at any
stage of discharge.
-
The second shortcoming is that the current, given by a transistor at some
known bias on its base/gate, does sufficiently depend on the temperature of
the transistor. For the current regulator not to "bend for the weather", both
transistors should be installed onto the same heatsink as close to each other
as possible. But still the temperature characteristics of transistors of even
the same type have some variations. And here we are to use completely
different ones. As the result the stabilization setting floats away with the
circuit heating up. It may go lower or higher dependently to the
characteristics of transistors taken and their position on the heat sink
relatively to each other.
-
The third serious drawback is that not any pairs of transistors are
compatible. One can easily understand, that if, say, current-setting shoulder
contains a germanium transistor (even with npn structure) and the forcefull
shoulder contains a silicon one, the circuit won't work just because the
voltage drop over the base junction of the germanium transistor will be never
enough to open a silicon one. Even more serious the problem is with MOSFET's.
The gate voltage needed to open MOSFET can vary to the large extent dependently
to the type of the MOSFET. As an example 'common MOSFET's' versus 'logical
level MOSFET's' can be used. They wouldn't work when isnstalled in pair to
the current mirror circuit. And still even in the limits of one class of
transistors there are no warranties too. A pair of common MOSFET's having
typical gate opening level or a pair of bipolar power transistors may appear
to be incompatible too. In fact it means that for each task (for each given
value of current stabilization and for each given feeding voltage) one should
carefully select a compatible pair of transistor types. Once he pair has been
selected (e.g. 2n2222 from Fairchild and 2N3055 from STM) one can reproduce
the circuit at any time with maybe minor corrections of current setting
resistor for each sample. But if one of the transistor types becomes
unavailable for some reason, You will suddenly find Yourself at the very
beginning of the road, with the necessity to redesign the circuit one again.
"And why on the Earth I need this circuit?" - You may ask.
The first answer is typical: The more variants of solution You have the
higher probability that You can elaborate the task successfully. The second
answer is a bit less trivial: this is the most low voltage circuitry among
the simple ones I know for these purposes. It lacks current sense resistor
in series with the load, and thus it lacks the voltage drop over it. If
the required control voltages are low enough (e.g. if it uses a pair of
bipolar transistors) one can feed a powerfull infrared diode from only
one Li-ion cell. Even when it is seriously discharged.
For tests and demonstrations this circuit was assembled. I'm not rich in bipolar
transistors, so the pairs were to be choosen from what was around. From what I had
I was able to select the compatible transistors only among pnp ones. In the
current setting shoulder of the circuit there stands russian kt644b transistor
and a pair of kt818g in the power shoulder. Why a pair? Because sole kt818g was
unable to permit the needed 3..5 Amps of current when the supply voltage was
3.7..4 Volts.

Besides this is another method to choose proper transistor. If You are unable to reach
current high enough, You can install several transistors in place of single one.
When R1 resistor in the current setting shoulder was 4 Ohms, the circuit stabilizes
3 amps, and when R1=3 Ohms it sets the current to about 5 Amps.
The next photo shows how a 5 Wt rated infrared diode works being fed by this circuit.

For now the power is not spectacular (after those NUBM08, NUBM44 and NUBM31T) but this
is not the sense. The sense is that the diode works successfully from a single Li-Ion
cell and the current is stable enough.
The next picture shows how to cook a current mirror on MOSFET's

It was said above that it is difficult to choose a proper pair of MOSFET's, especially among the logical level ones. It is because they have very different threshold voltage. To overcome this in the circuit above a 0.1 Ohm resistor was placed in series with M1 source. It helps to stabilize the operational point and to minimize the influence of threshold voltage difference.
The next photo shows how a 5 Wt rated infrared diode works being fed by this circuit. Note that only one Li-Ion cell is used.

 Return to contents Return to contents
PWM TYPE POWER SUPPLIES
↑
"Only seven notes in melody..." - they say when want to express that there's
nothin new in the world and any things could be invented are known already.
The same saying gets into mind when trying to get into the technique of
pulsed power supplies for laser diodes.
The number of possible variants of topology of circuit, allowing to pump
the energy from source with one parameters into some load with another
parameters, is not very high. I've counted 7 of them:
- 'Boost topology' (step up converter)
- 'Buck topology' (step down converter)
- 'Buckboost topology' (step up and down converter)
- 'Cuk' topology
- 'SEPIC' topology
- Flyback converter with transformer
- Forward converter with transformer
- Alternatives
Naturally there are even less of the really different variants, due to
the fact that Cuck, buckboost and SEPIC circuits are equivalent to series
pair of buck and boost circuits. One may find explanation of this here
or in Wiki articles found by keywords: Cuk, buckboost and SEPIC. A flyback
converter is logically a boost one, but with throwing the current from one
winding of its transformer to another via common magnetic flux.
Concerning alternatives, that includes many types of circuits with reactive
ballast, stabilizers with resonant tank circuit or any kinds of charge pumps
(including forward and reverse Marx banks), one may conclude that all these
circuits do not provide high enough efficiency while being too large and
weighty. At the end of this part we shall consider a few examples from this
area, but now let's return to the "mainstream".
To start with, let's consider a 'boost' topology. The next picture contains
its basic circuitry and current trace in its load.


To make the explanation easier one should remember that modern forcefull
field controlled transistors MOSFET's have negligible resistance of their
channel when they are fully open, and have almost infinitive resistance
when they are closed. So one can treat them just like a key.
The working cycle begins when positive bias comes to the gate of the
transistor. When open the transistor shorts the right (on the picture) lead
of the inductance to the ground (to the common wire). The inductance begins
to conduct a current, and to accumulate energy correspondently to the
E=L*I^2/2 law.
Then they cut the bias from the gate of the transistor. Transistor shuts
and disconnects the battery-inductance circuit. The current, having been
accumulated in the inductance, just has no other way to move, than to go
to the load through the diode.
Then the cycle repeats itself. They open transistor again and the right
lead of the inductance starts to be connected with the ground. But along
with this the left (on the scheme) lead of the diode appears to be connected
with the ground too. It means that while the transistor-key is shortened,
the current can not go through the load. One can see this on the trace.
Thus the 'boost' topology provides intermittent current through the load
and nothing except anti-ripple capacitor can cure this. Surely one can
modify the mutual positions of the load, key and inductance, but in this
case it will be something else rather than 'boost'.
Why the intermittent current is that bad? Generally laser diodes can be
fed with pulsed current, provided that their maximal allowed current was
not exceeded even in the peaks of pulses. However while the current is zero
(or too low) diode does not emit. So the average output power will be equal
to the power rating of the diode multiplied by duty cycle. I doubt that anyone
would buy a five watt rated diode for only to achieve some silly 1.5 watts
from it.
Why the anti-ripple capacitor is that bad? It would not be bad at all, if
laser diode had maybe a non linear but still monotonous dependence of voltage drop to the current. It's
a pity but it is not true in reality. At any moment, due to heating, or due
to back light, laser diode can suddenly increase its conductivity and the
anti-ripple capacitor will readily discharge into it to make an excess of
top allowed current limit. One can overcome this by installing some regulator
between the anti-ripple capacitor and the laser diode. For example one can use
an analog current regulator like one described <here>. However in this case
the main functions of current setting and current regulation belong now to
that additional regulator and not to the 'boost' circuit under consideration.
The next picture carries a basic circuit of 'buck' topology along with
trace of its load current.


Here the principle of operation allows to achieve continuous current in the
load without any anti-ripple capacitors. As the result this topology is of
wide use for any kind of current regulators for laser diode drivers. Several
variants of circuits of this type will be discussed in details further on.
The next picture depicts a basic circuit of 'buckboost' topology and
trace of its load current (at low duty cycle of control pulses, applied to
points A and B).


The circuit has two modes of operation. Conditionally speaking one of them
can be called 'boost-like', when most of the time transistor is in 'ON' state
and only for short periods they turn it "OFF", allowing the inductance to
pour its current to the load. In this mode of operation the current in the load
behaves mostly like current in common 'boost' circuit: it has shape of short
pulses with long pauses. It is obvious that this mode is of no use for laser
diode feeding for exactly the same reasons as it was in common 'boost' circuit.
Another mode of operation (let-s call it 'buck-like') appears when the
transistor is shut most of the time and allows the current in inductance-load
contour to circulate freely. And only for short intervals they turn the
transistor on to allow the inductance to accumulate energy from power source.
In this case the load current may be high enough during almost the whole
operation cycle. However in the contrast to 'normal' buck circuit, here
that 'almost continuous' current will still have short dropouts to zero.
During 'charge-up' periods the voltage of power source appears to be applied
through the open field transistor to the cathode of decoupling diode D1.
Moreover this voltage appears to be applied opposite to the current in the
load-inductance-diode contour. As the result this voltage causes the diode
D1 to shut and causes the intermittence of the load current.
It is understandable that this shape of current does allow to make a power
supply for laser diode at least in principle. The laser diode will be able
to output most part of its power without anti-ripple capacitor. However
one will meet some obstacles when trying to do it in practice.
The first to mention is noise. Noise of switching of the decoupling diode,
repeatedly applied opposite voltage through its non zero capacity, and so on. These noises not only make measurements more complicated, but also most of
manufacturers have the sole opinion that noises aren't make life of laser
diode any healthier.
The second drawback, making practical use of this mode not any easier, is
that the needed excess of feeding voltage is too high. To make the percentage
of the laser diode power available to be high, one needs to make the duration
of charging periods as small as possible. And in order for the inductance to
get enough energy in time, one needs to apply high feeding voltage. Usually
not less than triple of the voltage drop over the laser diode.
The third shortcoming is that at given frequency the 'buckboost' circuit
will require much higher inductance than normal 'buck' does. And it will
hit to the efficiency, to the mass, and to the sizes.
The only advantage of the circuit if the protection of laser diode, Indeed,
in case of failure of control of the transistor, or in case of its burning out,
the load becomes disconnected from the power source by the decoupling diode D1.
Hereby the current goes to the load only when the power supply works correctly.
And in case its burn the harm will be minimal.
Safety of laser diode is good thing, but the price to pay for this is not
very affordable. Worth to note that the safety is not 100% too. Imagine what
will happen if battery V1 was connected in reverse polarity? The MOSFET
would conduct without any respect to signal at its gate - its internal
diode conducts in this case. The decoupling diode D1 is also out of help here.
So if the power source is able to create enough voltage drop over L1 coil
(or even to burn it out), then the destruction of the load is sure. It is
evident, that one can connect another diode in series with the circuit to
ensure the correct polarity, but it is an additional measure, not relevant
to the circuit under consideration. Moreover, in a real circuit the contours
"battery-MOSFET-coil" and "coil-decoupling diode-the load" may be
interconnected via circuits of control and feedback, and it gives additional
weaknesses in the safety system. So, the 'buckboost' circuit is finally of
low use to be a main current setting and current regulating element of
laser diode power supply.
Generally the mode, where the current dropdowns are short enough and most
of the working cycle the current is close to nominal one, can be realized
in most of the circuits that provide intermittent current (SEPIC, flyback
and forward ones) but the drawbacks would be the same.
Cuck and SEPIC provide even more level of safety, because the load is
separated from their power source not by diode, but by a capacitor.
SEPIC circuit is shown on the picture below.

One can find the detail description of its operation for example here. Similarly to 'boost', SEPIC can not provide continuous or almost continuous
(with short dropdowns) current through the load. Correspondently, like 'boost'
it cannot serve as main current setting and current regulating element of
laser diode power supply.
CuK topology circuit ad its trace of load current in mode, nearly optimal to
feed a laser diode are given on the next figure:


One can see that the circuit allows to get a mode, where average current
through laser diode is close to its peak current. So the circuit is, at least
in principle, applicable as main current setting and current regulating element
of laser diode power supply.
However there are a few underwater rocks, waiting for those, who wants to
use it. The first: the separation capacitor C1 accumulates and stores electric
charge in process of operation of the circuit. If this capacity is large, the
accumulated charge may be high enough to destroy laser diode. C1 capacitor
behaves not exactly alike an anti-ripple one, mentioned above, but still
is hazardous to the health of laser diode. One may consider that the constant
component of the voltage across C1 may be treated as an incoming parameter
for the 'buck' stage of the circuit (it was already mentioned above, that 'CuK'
circuit may be imagined as 'boost' and 'buck' circuits, connected one after
another and with consequent optimization for number of parts used).
One of the bad effects of the charge, accumulated by C1, is that it brings
a delay into the current regulation circuit and may completely destroy the
mode of stabilization. If it happens the power sully becomes nothing better
than common voltage regulator and it is the direct way to burn Your laser
diode. On the other hand, if C1 is small enough, the circuit becomes more like
charge pumps (see below) with all their drawbacks.
With taking the slow charge, accumulated in C1, the dependence of current
through the load to the duty cycle of Cuk circuit becomes not only non-linear,
but even non-monotonous function, and it makes the task of current control
to be even harder to perform. (One can note here, that the dependence of
output voltage Vout to the duty cycle d_c for common CuK voltage regulator
is given by: Vout=Vin*d_c/(1-d_c), where Vin - is voltage of power source.
This function is monotonous and makes the task of voltage regulation to be
trivial).
Thus CuK circuit is the second (after 'buck') candidate to the role of the
main current setting and current regulating element of laser diode pulsed power
supply, if one is able (and wants) to overcome the difficulties in its
control. However as CuK circuit may be represented as sequentially applied
boost and buck circuits, one can treat this variant as a variety of the first
one.
Transformer based circuits provide even higher level of safety in case of
power supply failure. Generally they do not require any galvanic
interconnections between load contour and supply contour at all.
Circuit and load current trace for a flyback converter are, as usual, on
the picture below.


It have already been said that flyback converter is logically 'boost' one,
but with throwing the current from one winding of its transformer to another
via the common magnetic flux. Flyback circuit generally obeys the same rules
as the 'boost' one and similarly just cannot provide continuous load current.
So, like 'boost' it is unsuitable for use as main current setting and current
regulating element of laser diode pulsed power supply.
As to forward converter, due to the presence of transformer it generally
can not provide continuous current through its load too. There is, however
a special case - when the transformer is fed by 50% duty cycle rectangular
pulses and the load is connected via diode bridge.
One can ensure that any deviation of the feeding pulse shape from symmetrical
one (relatively to mean or weighted mean level) causes dropouts or even pauses
in the load current. It is illustrated on the next picture.

  
If one must keep the symmetrical shape of pulse to provide a continuous
current through the load, on can no more vary the duty cycle to provide
regulation. To feed the primary winding with trains of symmetric pulses of
variable duration is silly alternative too. The pauses between those trains
will cause pauses in the load current - there is no anti-ripple capacitor,
so the load current shape will repeat the ramp of the trains of pulses.
Now all the main variants of pulsed power convertors have been discussed.
It was found that only 'buck' converter is suitable as main current setting
and current regulating element. The buck, or circuits equivalent to it.
Thus if not taking into account roundabout alternatives, the modular scheme
of pulsed power supply for laser diodes can be reduced to sequential application
of three units:
- Primary power supply
- Voltage converter - regulator
- Current regulator based on 'buck' converter or equivalent.
In more complicated cases there may be present some control circuitry,
providing, say, adjustment of power of laser diode according to user
commands, or 'blinking' in one or another mode.

Primary power supply here means battery (accumulator) or mains rectifier.
Stabilized voltage converter may be designed according to millions of known
schemes. The main thing, it must perform, is to provide match between
electromotive force and internal resistance of the primary power supply
and the necessities of the unit, that performs current regulation. SInce
the load for the voltage converter is not capricious laser diode, but
rather tolerant buck converter, here You may use any anti-ripple capacitors
and filters You want. The voltage converter may be absent at all if the
parameters of primary supply are more or less matched with what is needed
for the pulsed current regulator. This scheme is of most use for portable
lasers, where size does matter. Accumulator battery serves as the primary
supply in this case.
Before we proceed to consideration of 'buck' type current regulators, I
want to mention yet another variant of laser diode power supply building.
It is a hybrid variant, consisting of pulsed voltage converter- stabilizer,
loaded by an analogue current regulator. If the DC-DC invertor provides
no more voltage than needed for normal operation of analogue current
regulator with no excess, one can expect that efficiency of the analogue part
will be high, and the heat output will be low.
The next circuit may serve as the example:

It consists of a SEPIC voltage inverter, utilizing 555-th timer as a PWM
controller, and transistor U2, used as the main switch. Coils L1 L2, capacitor
C2 and diode D1 form the barebone of SEPIC circuit. Further on is triple section
filter L3-L7, C3,C9, C10 goes, and its output is connected to analogue current
regulator, built according to a simple two-transistor circuit Q2, U3. The
latter circuit is described in details in the part SIMPLE ANALOG CURRENT REGULATORS.
Resistor R15 and filter R10, R13, R14, C11 are used to make path for feedback
signal, that drives Q1 and U4 transistors, which, in turn, cause changes in
duty cycle of the 555-th timer's oscillations. R7 R4 divider is used to tune
the circuit to the state, where the voltage, given by the pulsed part of the
scheme onto its analogue part, stops to rise when it becomes a pair of volts
higher than the threshold voltage, when current starts to flow through the
load (designated as Rload on the circuit).
The circuit was intended to feed a half of NUBM08 laser diode stack (4 diodes
450 nm 4.5Wt each) from 12V automotive Pb accumulator. SEPIC was chosen instead
of buck to provide the ability to use 24V accumulator too.
The results of assemblage and tuning have shown that the circuit is fully
operational. However even when the supply voltage of the analogue regulator was
barely enough for its operation, it still requires a heatsink for U3 transistor.
Moreover the selection of SEPIC as the DC-DC conversion was not fortunate. The
noise of D1 switch and other pulsed interferencies appeared to be so high, that
it required three stage LC filter (initially it was nit foreseen in the
circuit). As the result the device became cumbersome and have not found any
practical application. The results given by 'buck' current regulators were
far better.
Since the analysis given above shows special role of buck converters (for
not to say their unique role) for pulsed power supplies for laser diodes, let's
discuss this type of converter more closely. It consists of some control
circuit (so called PWM-controller), switch transistor and a coil an diode,
placed as shown on the next picture:

If one follows this layout straightly, there arises a problem of high side
switch. On the other hand it is not necessary that load circuit and control
circuit have common ground. If one avoids this the circuit may look like this:

No more high side switch problem.
Further on, for this circuit to become a complete current regulator, one
has to introduce some feedback, that will shorten the 'on' phase of switch
when the current is too high and prolong the 'on' state when the current is
too low. And the first that will be required for this feedback is some element,
giving a signal proportional to the load current. In the simplest case it might
be some resistor connected in series with the load:

Having introduced the feedback by this way we shall get some current
regulator based on 'buck' converter. Let's call it 'white buck'. Why exactly
'white' will be explained further on.
The given way to read the load current is certainly correct, but gives
a rise to several difficulties. First of all is that the signal from current
sense resistor is relative to the positive common wire, while most of control
circuits require the one relative to the negative wire. The problem of signal
level shifting is to some extent similar to the problem of high side switch
and generally has no simple solution especially for high supply voltages.
The second inconvenience of the described method of current sense resistor
connection is that the load appears to be not connected to any of the common
wires. Neither to positive nor to negative one. Why it makes so trouble? Let's
remember that the load is actually laser diode, despite the fact, that it was
designated as Rload on the picture. And most of laser diodes have positive or
negative terminal electrically connected with their casing. Moreover, in most
popular designs of lasers they put laser diodes directly onto some wall of
metal casing. Both facts cause the situation, where the casing of the laser
device authomatically becomes a common wire (or at least backs it up).
If one then wants to introduce a current-sense resistor to between the
diode and the common wire, one needs to insulate the diode from the casing.
It is not trivial task and get ready to loose the efficiency of the heatsink.
While looking onto the circuit one may note that when the transistor is open,
its drain current is almost equal to the current through the load. And when
the transistor is shut, the load current can never exceed the one, that
was when the transistor was still on. So, with some minor loss in precision
one can severely gain in robustness if the current-sense resistor was moved
outside the L1-D1-Rload contour:

Users of internet forums often call this topology 'blackbuck'. Strictly
speaking this term is not commonly established one, but still it is
rather wide spread and very handy. Here I will use it further on.
In the 'blackbuck' topology the current-sense resistor is outside of
the contour with load, so the measurements are a bit incorrect, and one
can say that they are conducted in the 'black' way. On the contrary,
when the current-sense resistor is inside the contour with load, one
can say that the measurements are done in the 'white' way and call this
topology as 'whitebuck'. This explaines the name, having been used earlier.
As a control circuit for whitebuck or blackbuck one can use one of
numerous chips, known as 'PWM-controllers'. One can also use any other
circuit, provided that it contains comparator, Schmitt gate, and a delay. Proverbial 555-th timer chip contains all these components and is commonly
used as a simple PWM controller. One should however remember, that laser
diodes are usually powerful load and to feed them a circuit with external
powerful MOSFET is needed. 555-th timer has poor load capacity of its
output terminals and thus require external buffer stages or special
driver chips to control the MOSFET at the frequences needed.
GATE DRIVER INTEGRATED CIRCUIT - IS A TINY AND COMPARATIVELY
INEXPENSIVE CHIP COMMONLY USED TO REPLACE A CUMBERSOME HEATSINK OF YOUR
MOSFET
There are plenty of gate driver chips, that can provide the necessary
speed at the currents required. One can mention TC442x, MIC442x, UCC3732x,
1EDN75x, ixdd414 series. Dont bother with something like IR21xx - maybe
they work good with high voltages, but they are too slow for our 'laser'
purposes.
The desired conversion frequency is like 200..500 kHz. In this range it
is high enough to provide small sizes of the circuit, and still low enough
for many common ferrites to operate with, and for the time of MOSFET switching
to be negligible with the working cycle period.
An example of 'blackbuck' current regulator is given on the picture below.

The circuit is made in a 'good manners' style of pulsed power force
electronics: each stage has decoupling over its power line (D1 diode and C2
capacitor for master oscillator on 555th timer, D2 diode and C3 capacitor
for 4420-th gate driver stage), the gate of U3 transistor is 'grounded' through
R7 resistor to avoid spontaneous opening due to statics, when outputs of
4420th are shut. The power line of 4420-th is shunted not only with
electrolytic capacitor C3, but also by a ceramic one C4 (100nf). C4 should be
mounted directly to the legs of 4420th. Feedback signal is filtered by
R8C5 from the high frequency interferencies. In addition to this the schematic
explicitly shows the current sense resistor being formed by four resistors
(R3, R4, R5, R6) connected in parallel and each having the resistance of 1 Ohm.
One can set the desired current of laser diode by connecting and
disconnecting the necessary number of resistors. Further on in this text
the current-sense resistor won't be drawn in such a details. If in this place
of circuit You see 0.25 Ohm resistor, You should get it as: "for resistors,
one Ohm each, connected in parallel, and measures are taken to make it possible
to connect and disconnect any of them at any desired time."
I seriously recommend You to use LMC555 chip as a 555th timer. This chip is
logically full analogue of the common NE555, but it is made with CMOS
technology and it is able to operate at frequences as high as 3 MHz. Common
NE555-th are either not operational at all at the necessary frequences, or
just unstable. MOSFET may be of any kind, intended for 20 or more amps of
current and 20 or more volts of supply voltage. IRLU2905(IRLR2905) is
interesting due to it has little resistance when open and occupies a small
casing DPAK(IPAK). Additionally this MOSFET has logical gate level, and,
though it is not completely necessary, it is very useful from many points of
view. As for D3 diode - You can use any Schotkey, rated to 5 Amps or more.
Its reverse breakdown voltage is of low importance here, but still it is not
very good idea to choose it below 30 Volts.
Having assembled the 555-th stage check it for oscillations. In the absence
of feedback it should give rectangular pulses with repetition rate of
100-200 kHz. Duty cycle should be 80-90%. If the frequency differs too much,
adjust value of C1 capacitor. If the chip does not oscillate, or duty cycle
is too low, adjust the R1/R2 divider. R1 and R2 values on the picture are
related to LMC555 as the timer and 8.4 Volts power supply (two Li-Ion
accumulators in series). If using another type of 555 timer or very
other supply voltage, most probably You have to adjust the divider.
Remember, that the duty cycle is in non-linear dependence on the R1 to
R2 ratio. Also, when R2<2*R1 the circuit does usually not work.
When settled with 555, assemble the 4420th gate driver's stage. Check its
proper operation, by loading its output with some 5-10 nf capacitor instead
of the real MOSFET gate. The driver should transmit the pulses properly.
Rise and fall of them should not be too long, and there should be no 'ringing'.
Then assemble the forcefull stage on MOSFET, and add the feedback loop (R8,
C5, Q1). Attach an 1 Ohm resistor to the output instead of laser diode, and
let only one from the set of current-sensing resistors to stay connected.
Turn the power on. Measure the current of the load and duty cycle of 555-th
timer. The output current should be somewhere around 0.5 Amp, and duty cycle
should be much less than it was for the free oscillations. Shrinking of the
duty cycle is the result of feedback loop operation. If it does not function
properly the circuit will not provide constant current.
After the full assemblage and preliminary tests, check the quality of
current stabilization. Attach 0.5, 1 and 2 Ohms to the place of load. (Only
one at a time! Clever ones, - sorry for this note.) The output current Will
change with change of load (it's normal ' cause it's not a whitebuck). But
this change should be not over 20%. Also check for the absence of surges
during turning the battery 'on' and 'off'. (For this to perform one should
have a memorizing oscilloscope. Note that some digital scopes have poor or
even inoperational 'single' mode. These scopes are out of help here.)
Check if the ripple amplitude is good for Your purposes. The ripple amplitude
is tied directly to the ratio of L1 inductance to the resistance of the load.
If the ripples seem too large for You - choose higher frequency (by making
C1 smaller) or increase L1 inductivity. Keep however in mind, that with too
many of turns You risk to hit the ferrite core saturation. The circuit
will loose operationability if this happens.
During measurements You will suffer from pulsed interferences. The cheap
'household' oscilloscopes usually have poor shielding and they can show
false surges. If on the nice background of fine zigzag of current in the load
You see sharp needles, several amps in amplitude and 10-100 ns in duration,
remember that they physically can not exist. L1 inductivity is just unable
to let them pass through the load.
After having been convinced in the correct current regulation and absense
of the surges during turnin on and off (and also during mechanical shocks)
You can replace the load resistor by a real laser diode. The circuit is
designed to feed laser diodes by currents in range of 0.5-5 Amps. Most
single powerfull diodes match this range. The voltage drop across diode is
not very sufficient. You can feed GaAs (red and infrared) as well as GaP
and GaN diodes (blue, green and ultraviolet). If one wants to use the circuit
to feed numerous diodes connected in series, the circuit must me modified.
Further simplification and size reduction may be achieved if one gets
rid of the separate master oscillator stage (on 555-th timer or other
PWM-controller). Note, that gate driver does already contain comparator
and Schmitt's latch, so the gate driver itself can be a decent oscillator.
Blackbuck topology circuit using 4420 (non-inverting) gate driver is shown
on the next picture.

As You can see in order to reduce the PCB footprint, elements of decoupling
of the 4420-th stage from the forcefull part were omitted here. The current
sense resistor is also shown in a brief foem - as a single resistor. Resistor
R4 is optional. It is used to prevent too much of gate ringing. If Your sample
of circuit does not suffer from this You can omit it. If You want make it as
small as possible, and if its supply voltage is low, You may omit D3 diode,
which is used to protect the base of Q1 transistor from reverse voltage. You
can even omit C4 capacitor, intended only to make the range of oscillations
wider.
As earlier C3 capacitor is to be mounted directly to the legs of the gate
driver. The requirements to the powerful MOSFET an to D1 diode are the same,
as they were in the above circuit on 555th timer. D3 diode can be of lower
power: ~1 amp rated and 20V of reverse voltage. Almost any signal npn silicon
transistor can work as Q1. Keep an eye, however, that its allowed collector
current should be not less than 50 mA, and its allowed collector-emitter
voltage must be at least several volts higher than the voltage of Your
battery. At higher voltages, to keep the collector current in safe limits
one might need to increase R3 value. This affects the behavior of the circuit
in rather complicated way. One could say that it shifts the range of loads,
where stabilization is effective, towards higher resistances. Usually it
is not desirable and should be avoided, so You might better to consider
using a more powerfull transistor in place of Q1 rather than increasing R1.
If using SMD-components one can make the circuit as small as 25x15 mm,
that allows to place it into a body of powerful laser pointer.


I'm not specialist in the area of ferrites, so i cannot advice any good
on L1 coil winding. You should either buy a ready choke rated to 15-20 uH
and 5 Amps of current or to choose the right ferrite core by Yourselves.
Dependently to the ferrite used, the number of turns may be in range of
5-15. The wire should not be too thin. Enameled copper wire having diameter
of 0.5-0.75 mm gives good results.
On the contrary to the previous circuit this one is a sole and complete
stage and cannot be debugged by parts along with its assemblage. Having
soldered it up, connect an ~1 Ohm resistor to its output instead of laser
diode. Set the current-sense/current-setting resistor R1 to 1 Ohm to begin
with. Turn the circuit on and observe the oscillations with an oscilloscope.
If there is no oscillations, try to increase the capacity of positive feedback
capacitor C4. (Generally the oscillations should be, and their absence mean
something gone seriously wrong. Trying to enforce them by C4 is like trying
to revive a dead body, but all is up to You though.) When the self
oscillations are stable, adjust C1 capacity to set their frequency into the
correct range. Generally R3-C1 works as frequency setting chain? use it
to make it in between 200..400 kHz.
Proceed then to the measurements of current stabilization quality,
When load varies in range of 0.5..2 Ohms the current should vary not more
than by 20%. Generally most of the said about tuning of the circuit on 555th
timer applicable here too.
After all adjustments and checks for absence of surges You may connect
a real laser diode to the output of the circuit.
In the given form the circuit allows to feed single laser diodes with current
in between 0.5..5 Amps. If one provides an independent power source for
4420 chip and Q1 transistor, and then to increase the supply voltage for the
forceful part, the circuit becomes able to feed garlands of laser diodes
connected in series:

If Your battery is of low voltage type and Your laser diode is of nitride
type, it may be not so simple to convince the circuit to give more than 3 Amps.
(Indeed, two lithium-ionic accumulators may mush down to 6 volts under the
heavy load. Voltage drop across the laser diode itself is around 4.5 Volts.
Finally the circuit itself has only 1.5 Volts 'to hum'. To reach, say, 5 Amps
the sum of all stray resistances must then be less than 0.3 Ohms. Subtract
the current sense resistor value and You will get 0.2 Ohms for all the
circuitry, including MOSFET's channel, the coil and the strips on the
PC-board.)
However one could easily solve this, because 'blackbuck' topology drivers
are easy to parallel. For better stability one should add decoupling diodes
at their outputs? as on the following picture:


Next to the schematics there is a (simulated) scope trace of the current
through the laser diode. Right and left 'blackbucks' were turned on and off
not simultaneously, and it can be seen on the trace.
Since the circuits operate independently, their sum current ripples have
shape of beats between the frequences of oscillations of both circuits.
In their maximum they can be the arithmetic sum of ripples given by each
circuit. This fact should be taken into account when using several drivers
in parallel. One should either increase the safety margin when selecting
the necessary current for laser diode or take measures to reduce the ripples
(increase frequency or increase inductances L1 and L2).
Whitebuck topology circuit is better to be assembled using an inverting
gate driver (like 4429):

Current-setting and current sensing resistor here is R3. The principle of
operation is very simple: as soon as the current through the load reaches the
certain value (defined by R3 value) Q3 transistor opens and gives positive
bias onto the entrance of inverting driver. This shuts the MOSFET and causes
smooth decreasement of current through the load. After the current has become
less than the preset value, the gate driver can not switch to on instantly,
because the positive bias at its entrance is 'memorized' by C1 capacitor.
Only after its discharge via R1 the circuit can connect the supply voltage
to the contour of the load - the working cycle repeats itself.
Aside of the general shortcomings of all whitebucks (that load has no common
with common wires) this particular implementation of the circuit has numerous
drawbacks of its own. The problem of signal level shifting is solved here by
the most simple way: with a help of a stage on pnp-transistor Q1 with load R1.
This simplicity begins to cause troubles when supply voltage goes higher. And
if the circuit works best when the supply voltage is 8.4 Volts (2xLi-Ion), it
becomes hard to get the necessary duty cycle at 12 Volts of supply. At 24 and
of course at 36 V the circuit becomes inoperational. Note that LTSpice
simulator does not discover this problem. Further on, in order to get the
proper dependence of the duty cycle on the load value, Q1 transistor has to
have a smooth transient characteristics. Russian KT3107 works well here, and
its (said to be) analogue 2N3906 - does not.
One may ask, why mention this circuit if it has so serious shortcomings?
The answer is that any mice trap contains its own piece of free cheese. The
main advantage of this circuit is that it makes the current to stay as
wolverine tail in frosty night. If it was normal for blackbuck circuits to
change the current by 20% when the load changes by 4 times (from 0.5 to 2
Ohms), for 'whitebuck' scheme it is hard to note any change of current with
'household' measurers during the same load variations. Keep in mind, however
that if its supply voltage changes strongly (e.g. from 8 to 12 volts) one may
need to recalibrate the current setting resistor.
Due to the fact that circuit behaves poorly with increasement of the supply
voltage it cannot be rearranged to some 'high voltage' variant to feed garlands
of laser diodes (as it was with 'blackbuck').
There are some specialities with its paralleling too:


One cannot connect together any common wire of the circuits. And the
decoupling diodes are the must here.
The given circuits certainly do not cover all the variety of 'buck'
converters or equivalent to it circuits. There are all kinds of self
oscillating ones like the above on 442x, and all kinds of externally driven
ones (like the one with 555timer). Control circuits and logic of feedback
operation may be very sophisticated, including tenth of protections and
limitations.
A separate attention is to be paid to multiphase circuits. It was said
above that several pulsed current regulators may be connected in parallel
to a common load. However in the discussed case the drivers worked independently
and their ripple voltages summated. And if several pulsed current regulators
are united by common control circuit, that enforces each regulator to be
in 'on' state only while others are in 'off' state, the resulting scheme is
called as 'multiphase' one, and the ripples are no more to be added to each
other. The power of this approach is so high, that even a multiphase 'boost'
converter may yield a decent source for a laser diode. However the price
is high too: N phases mean N MOSFET's, N gate drivers, N coils, microcontroller
and two or even three levels of power supply voltage (5V for logics, 12V for
gate drivers and, say, 30 V for the forceful parts). Microcontroller appears
here because the complexity of the control logic for all this husbandry is
so high, that in our times the only reasonable way to perform it is
programmable control. One can easily imagine that there is no way to compress
all these things into a casing of some silly laser pointer. The expenses
become high too. It means that for portable lasers one can possibly not look
at the side of multiphase controllers. However if Your task is to feed the
array of say 20 diode bars, each rated to say 100 Amps, multiphase technique
may become the only fruitful solution
ALTERNATIVES
There exists an old good scheme of laser diode connection, that is used widely
even now, but mostly in the cheapest (keychain) laser pointers. It is
connection of the laser diode to power source through a resistor:

If R1 resistance is much higher than the resistance of the diode, the current
through the diode will be to the most extent determined by R1 value and
V1 voltage. Strictly speaking such thing as 'resistance of laser diode' is
volatile and unknown, and one can only speak about some 'mean' resistance,
being equal to the voltage drop across the diode in its nominal state divided
by the current through the diode in the same state. One may also hope that
the true resistance of the diode fill differ from the mean one not more then by
2-3 times.
Why this approach is bad? Only due to its low efficiency and beastly high
amounts of heat. Let's assume that we use NUBM44 laser diode. At working mode
the voltage drop across it is about 4.5 Volts. Its operational current
is ~4.5 Amps. It results that its mean resistance is about 1 Ohm. Let's take
that we've chosen the ballast resistor value to be 10 times higher,
i.e. R1=10 Ohm. Then to provide 4.5 Amps of current we have to apply the
electromotive force of ~50 Volts and the heat power on the resistor will
slightly exceed 200 Wt.
The first thing that comes in mind when looking at this circuit is that
it is possible to avoid such losses by replacement of the active resistance
by reactive one. It is well known that (an ideal) reactive resistance does
not convert the applied electric energy into the heat. As a reactance one
could use a choke coil or a capacitor. Many of us have already seen a circuit to
feed a luminescent lamp with a choke, or at least many of us know about it.
Its principle of operation is exactly the same - limiting of the current in the
load by some inductive resistance, that does not introduce losses.
The next figure shows a variant of circuit, that uses a capacitor as
a reactive ballast. In order for the reactive resistance to work, one needs
to feed the circuit by an alternating current, so don't get amased when
see a diode bridge as a rectifier on the picture.


So where is a rectifier, there should be an anti-ripple capacitor too.
In order to keep the accumulated charge small (to keep laser diode safe) one
has to choose small values of the capacity. 100 nf looks like appropriate more
or less. But with such a capacitor we need to apply incredibly high frequency
(like 100 MHz) to keep the ripples low.
There also exists a three-phase rectifier, that allows to get rid of the
anti-ripple capacitor without respect to frequency:


It allows to use much lower frequency, but requires a THREE phase radio
frequency generator, three ballast capacitors and six powerful ultrafast diodes.
In the circuit with inductivity as a ballast element the things aint better.
Thus the evident simplicity and efficiency of the circuit with reactive
ballast turn out to be deceiving.
Another attractive variant is a stabilization of current using a resonant
tank circuit, as it is shown on the next picture:

The current through the load is here determined only by the voltage of the
power supply and by the impedance of the tank circuit. It is almost independent
to the value of the load itself in a very wide range of loads. However it is
only in ideal case. When we take into account the finite q-factor of the tank
circuit and the finite precision of aiming the supply generator frequency to
the resonance point, the things become much worse. Indeed, why the voltage on
the leads of the load resistor does change when its resistance is changed? It
is only due to oscillations in the tank circuit. If R1 is high the tank circuit
is weakly shunted and its q-factor is high. The voltage becomes high too and
it provides the necessary current through the load. On the contrary if R1 is
small the tank circuit is strongly shunted and has low q-factor. The amplitude
of oscillations there becomes low, and keeps the current through the load
at the desired value again. It gives current stabilization. However if the
q-factor of free LC tank circuit is low and the driving frequency differs
from the resonant one, it drastically affects the quality of stabilization.
The separate disgusting speciality of the current regulator based upon a
resonant tank circuit is that it behaves poorly, when fed by rectangular
pulses. All deviations of the feeding voltage from the ideal sin(w*t) affect
the quality of stabilization. From the other hand You will want Your RF
generator to operate in switching mode, just to provide its efficiency.
Things are even worse, if the output of the circuit is loaded onto a real
laser diode rather than to an abstract resistor. Again there appears a
rectifying bridge, again the anti-ripple capacitor, and again the requirement
to keep the ripples low together with low value of anti-ripple capacitor means
very high frequences (the same 100 MHZ as in the previous example).
Principle of operation of a charge pump is illustrated by the next picture:

C1 capacitor is periodically connected to power source V1 and then to the
load. Each time the capacitor is connected to the source, it accumulate the
charge q=C1*V1. Easy to get, that the current through the load just can not be
any higher than C1*V1*F, where F is switching frequency. Thats all of the
principle of stabilization (or at least limiting) of the current. By changing
the frequency and/or the supply voltage we can vary the current through the
load.
It may be not so obvious, but the circuit is in general equivalent to the
one with a capacitive ballast (see above). Except maybe that it is fed by
rectangular pulses and not by sine wave. From here it follows that all
drawbacks of the first variant are present here too: intermitted current
through the load, anti ripple capacitor can not be avoided, and too high
frequences to keep the capacity of the anti-ripple one low.
The example above can not exhaust the tremendous amount of alternative
circuits art. E.G. one can mention a circuit, where ballast is formed by
a limited magnetic flux in a specially designed transformer. A set of physical
phenomena, that can provide current limiting, is probably unlimited. However
none of these circuits was able to compete with the 'mainstream' consisting
of a pulsing voltage regulator and stabilizing 'buck' converter, which was
discussed here in the previous section of this part.
CONCLUSION:
- Buck converter is a very suitable circuit to make high efficiency pulse
width mode current regulator for laser diodes. There are some other circuits
that behave like buck, but more troublesome to control (CuK converter)
- Most of other circuits, with intermittent current do have a mode when
current dropdowns are short enough, but this mode makes this circuits
to look more like immature buck converter, then why to pay more and not
to use a real buck?
- Alternative arts of electronics are too immature to offer a real alternative
to the classic approach.
 Return to contents Return to contents
SOFT START
↑
Usually it is hard to implement a so called "soft start" in self oscillating
circuits. "Soft start" is the mode where the current in the load approaches its
nominal value smoothly rather than instantly. In relation to the pulse circuits,
where the onset rate is principally limited by inductance, one can say that
"hard start" is when the current reaches its design value in the first peak of
oscillations, and the "soft start" is when the current reaches its design
value after several (tenth of) peaks have passed.
It occurs, that almost in any kind of current stabilizer one can implement
the soft start with a help of the next simple circuit. The load is shown in
the shape of laser diode for clarity.

It is essentially the common (and unloved) anti-ripple capacitor connected
in parallel to the load. However unlike the common case, it is connected
via resistor R1 rather than directly. For the circuit to operate properly,
the value of this resistor should be close to the equivalent resistance of
the load. In case of laser diode the load resistance is equal to the voltage
drop across the diode (U(LD) on the picture), divided by the current through
the laser diode (I(LD) on the picture). The voltage drop and the current
should be taken as known for the nominal ratings of the diode. For powerful
blue diodes like NUBM08 and NUBM31T this value is slightly more than 1 Ohm,
and for NUBM44 is slightly less (for one diode). For 5 W rated infrared diodes
typical equivalent resistance is about 0.5 Ohm.
With knowledge of R1 value and of the necessary onset time (tau on the
picture above) one can easily estimate the necessary C1 using the well known
relation: tau = R1*C1. Typically C1 is between several microfarades to
several tenth of microfarades.
Resistor R2 is needed to discharge the buffer capacity C1. Dependently
to the circuit of laser diode driver being used, it may be needed or not needed.
However it eats not much of current and occupies not much place, so it is
better to leave it in place. Just in case.
The complete circuit including the laser diode driver may look, for example,
as this:

The picture shows how to feed one branch of NUBM31T array from 30V rated
Li-Po accumulator. (5 laser diodes in series.)
The advantage of this circuit is clear enough: it allows to get rid of
peaks and excesses at the initial time after the driver was turned on.
It drives the laser diodes to their operational state smoothly and this
prolongs their life.
The disadvantage of the circuit is that the time constant of the driver
reaction to the changes of the equivalent resistance of laser diode becomes
higher. The buffer capacity in this circuit resembles some anti-ripple cap
of the common voltage rectifiers or rough current regulators. That's why if
the laser diode decides to suddenly decrease its resistance, the accumulated
charge from the buffer capacity will certainly flow through the laser diode,
trying to exceed the maximum allowed current. Unlike the typical case of the
anti-ripple capacitor, here the situation is alleviated by the fact that
the buffer capacity is connected through a resistor. It means that even if
the resistance of the laser diode has dropped to zero, the current would be
limited anyways. However this is not the warranty of laser diode survival,
this is just an increasement of the probability. The question, whether to
use the discussed soft start circuit or not, should be decided in each
case individually.
The fact, that arsenide laser diodes can be successfully fed from drivers
with low speed (e.g. based on LM317 analogue chip), shows that these diodes
have no tendency to vary their resistance rapidly, strongly and suddenly. It
means that one can more or less safely use the discussed circuit with arsenide
diodes (with one exclusion, see below). On the other hand nitride diodes got
busted (both in direct and figural sense) with their tendency to change their
internal resistance, so one should be especially careful with them, when trying
to apply this circuit.
However the circuit was tested for feeding NUBM08 and NUBM31T diodes. It has
shown good results. Typical oscilloscope trace of the turn-on process is shown
below (the dip on the trace is ringing of the mechanical switch, note that
inspite of ringing the limiting current was not exceeded).

It should be said specially about the case, when it is poosible that a
significant amount of the irradiated laser light comes back to the laser
diode. It is exactly the case, when laser diode can (and will) change its
resistance rapidly, strongly and suddenly. It oftelnly happens when trying
to cut well reflecting metals. Note, that they don't need to be polished -
in any case there appears a pool of molten metal and it is hard to predict
how it will reflect the beam. To avoid the otiose lines one can recommend
to just not use this circuit of soft start, when a significant part of laser
light is possible to be returned back to the laser optics.
THE LASER DIODES
↑

When choosing/buying a laser diode one should pay attention to:
- Power
- Brightness
- Color (wavelength)
- Lifetime
Power is the main parameter of the laser diode if You are going to cut or
drill something with the diode. E.g. to cut plywood on a CNC machine. A diode
becomes reasonably suitable for usage in CNC machining beginning from 5 W of
power (well at the bare least - from 3 watts of power).
For the usage as a laser pointer the factor of the most importance is the
brightness. The visual perception of brightness is also affected by color. The
perceived brightness of the spot of green laser pointer (532 nm) is almost 10
times higher than the perceived brightness of blue (450 nm) or red (650 nm)
laser pointers, and this is when the output power (in watts) is equal.
If we drop away those twisted photometric values, then the brightness will be
just the output power divided by the (3d) divergence angle and by the area of
the light emitting surface. And in this sense the brightness does almost
directly determine the range of the laser. It means not only the ability to
point to a monument 5 miles away from You, but also the transmission range
of You photo-phone using the diode as its transmitter, and the ability to
light a match at the distance of 15-30 feet.
If You need range - choose brightness even to the detriment of power.
The brightness is kinda reverse value to the entropy. One can not increase
it without the work of the applied forces. On the other hand there are much
and many opportunities to decrease it down.
In order to determine the brightness You need to know the power of the diode,
the divergency of its beam and finally the sizes of its emitting surface. Here
are the internals of the common diode without its top cover:
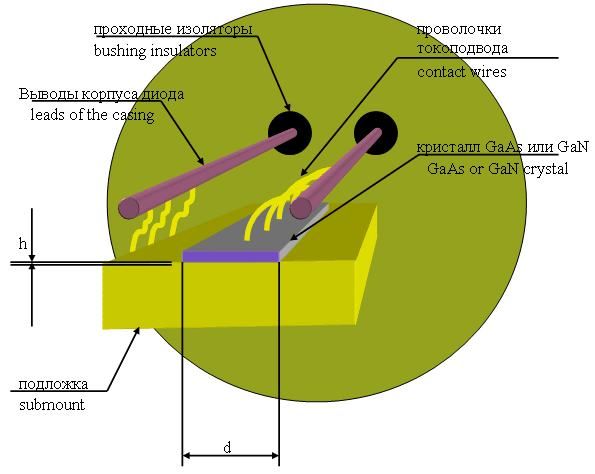
The emitting surface is characterized by its sizes h and d. The height h
is the thickness of the pn-junction. And one can estimate it as being almost
equal to the working wavelength. The width of the emitting surface is sometimes
not equal to the width of the semiconductor crystal (as it shown on the
picture). Usually one can get this value from the datasheet, If there's no
datasheet treat it as if it was equal to the width of the crystal. If You have
a possibility to turn on the diode and You have a lens with You, the next
simple experiment will allow You to discover the width of the emitting area:

Focus the radiation of the laser diode onto a screen (onto a wall in the
simplest case). Better not to use the full power to avoid burning of anything.
Try to achieve as sharp image as possible. Then measure the distance l between
the diode and the lens, and the distance L between the lens and the screen.
Also measure the size of the strip of light on the screen D. Finally You can
get the size of the emitting area d from the following obvious proportion:
D/d = L/l .
Concerning the divergency, one should keep in mind that laser diode has
two very different directions of divergency. If taken without any (internal
or external) optics the laser diode will show its spot in a shape of an
elongated rectangle:

Along the axis orthogonal to the plane of the crystal (to the plane of the
pn-junction) the angle of divergency O_|_ is large. Usually it is 60 or even
90 degrees. Thus this axis is named "fast axis" (the axis along which the
beam diverges fast), and the angle itself is named "angle of divergency along
the fast axis".
Along the axis parallel to the plane of the crystal the beam diverges slowly.
8 to 12 degrees usually. So the axis itself is called "slow axis".
The fact, that the divergency along the slow axis is lower than along the fast
one, does not mean that the "beam quality" is better in this direction.
If we consider 2D problem in the plane, that contains the fast axis, we can
understand, that in this 2D problem the laser diode can be treated as practically
ideal pint-like source of light. And thus the radiation can be shaped into an
almost ideal parallel beam, limited only by diffraction and aberrations of the
lens.
Another situation if we consider 2D problem in the plane, that contains slow
axis. Now the source has certain (and not negligible) size. And when You will
try to focus the beam onto a far away screen, You always will deal with the
image of the source (as it was on the picture on the determining the size of
the emitting surface). One just can not make the spot to be smaller than that
image.
That "foolish" beam shape makes the life worse if one needs to focus or to
collimate the beam. (Collimating is the process of making the beam to be as
parallel as possible. Usually it is done by a lens, by installing the emitting
area of the laser diode into one of the foci of this lens. The lens, being
used in collimating purposes is known as "collimating lens" or simply as "collimator".) To perform this task one generally needs an astigmatic optics -
cylindrical lenses or anamorphotic prisms (see further in the OPTICS part)
however those parts are less affordable and cost higher than the common
(spherical) optic parts.
To make the life easier for the ones, who does not want to deal with the
astigmatic optics, the manufacturers produce diodes equipped with internal
cylindrical lens, that partially compensates the fast axis divergency. That lens
is called "Fast Axis Compensating lens" or simply FAC-lens.

Don't think that FAC lens is able to increase the brightness of a laser diode.
The decreasement of the fast axis divergency costs the serious drop of the
beam quality. In most cases You can treat it as if the diode with FAC lens has
the enlightened area of the FAC lens as its emitting surface. And it is much
larger than the pn-junction area.
Consider the example. Lets assume that the initial diode without any lens has
the size of its emitting surface of 20x200 mcm and the power of 5 wt. Then
using a lens with 100 mm focal length You will be able to focus its beam into
1x10 mm sized spot at a distance of 5 meters. It corresponds to 50 W/square cm
intensity, which is enough to puncture a paper, to light a match and to make
many other useful things.
If the same diode was equipped with FAC-lens, having a shape of a cylinder
100 mcm in diameter (this can be often seen in practice), You can assume that
the emitting area now has the size of 100 x 220 mcm. (The last number has
increased due to the aberrations of the cylindrical lens.) If You again use
a lens with 100 mm focal length, You will be able to obtain only 5x11 mm spot
at the same 5 meters from the diode as it was in the first case. The new
intensity will be only 9 watts per square centimeter. I.e. five times worse
than it was in the paragraph above.
However in the first case You need a pretty large lens, moreover the one
having its diameter being equal or more than its focal length. (The minimal
diameter of the lens should be taken from the condition, that the lens should
capture all the light emitted from the diode, and, hereby, is determined by
the fast axis divergency.) On the contrary in the second case You need a lens
with 100 mm focal length and 20-30 mm diameter. Such a lens is cheap and
affordable.
I hope, that this example has shown that it is hard to say, whether to choose
the FAC lens or not, without knowing the details of the application and without
taking into account ones possibilities to assemble the proper optics. Generally,
if You need to cut and drill something in 3-5 cm in front of Your diode, it is
more wise to choose diode without FAC lens and rely on the abilities of good
spherical optics. Otherwise, if one needs high range, and if the possibilities
of using the astigmatic optics are limited, one should better choose diode with
FAC lens installed.
Color (wavelength) affects not only the perceived brightness of the laser
spot. The absorptive ability of the material depend to the color strongly.
The amount of absorption means the amount of energy available to cut or drill
the material and therefore determines how easily or hard it can be done.
A classic example is white paper. One can easily puncture it by a blue laser
pointer. Not so easy it can be done by a green one. And with a red one it
is very very difficult.
Nevertheless from the point of view of materials processing the color is
still secondary factor after the power. It is because organic materials can
easily be charred, and after that they absorb almost every wavelength. Metals
may be painted and/or annealed to increase their absorption. And glass...
if it is colorless, it makes no difference between red or blue - any visible
lasers are useless to process it.
From that can be observed now on eb@y and aliexpre$$ one can come to the
conclusion that there are the next kinds of diodes:
- Invisible infrared type (920-980 nm) - their power is up to 10 W and they
cost like ~30 USD/W
- Visible infrared ones (700-820 nm) - their power is up to 10 W and they
cost like ~30 USD/W
- Red ones (of different color in range 630-670 nm) - with power up to 1 W
and cost ~ 40 USD/W
- Green ones (520 nm) - with power up to 1 W and cost ~ 80..90 USD/W
- Blue diodes (440 - 460 nm) - with power up to 6 W and cost < 18 USD/W
may cost <9 $/W if in stacks like NUBM06-NUBM08
- Violet ones (405 nm) - with power up to 1 Wt and cost like 35 USD/W
It is understandable, why green diodes cost so much - they appeared recently
and there is still deficiency of them. Less understandable why red diodes still
cost high and have rather low power despite the fact that they were the first
to appear at the market.
Infrared and red diodes are made of Gallium Arsenide (GaAs). Actually there
is a puff-pastry inside them. It is so called "heterojunction". However it has
nothing to do with DIY skills, so it is simplier to consider that these diodes
are based on GaAs only. Green and blue diodes are made of Gallium nitride: GaN.
What does this knowledge mean for DIYer? For example one can try to tie the
known special properties of the diodes with the material they are based on.
It was said above that all the Gallium Arsenide based diodes, I had, did
operate well when fed by a current regulator, based upon on-chip voltage
regulators, like LT1083 and similar. There was no
exclusion. It means that their current-voltage curve is of non-decreasing type.
On the other hand the fails with those drivers took place and blue diodes. If
it is due to the properties of the semiconductor, one can suppose that all
nitride diodes (blue, violet and green) have the property of dynamic variation
of their resistance. And thereby they cannot be fed by any kind of driver
having a large capacity at its output.
Another observation - different temperature/overheat endurance of the diodes
of different types. I personally have sent a few arsenide diodes to the heaven
by powering them without a proper heat sink. It even happened that these diodes
went to their ancestors just after overheating in the process of soldering.
Nitride diodes haven't yet been noted in such a behaviour. Nichia, for example,
allows operation of their diodes at the temperatures up to 70°C, and storage
at the temperatures up to 85°C.
The higher heat durability of the nitride diodes is not necessary directly
related to the semiconductor properties. It may, for example, be determined
by the types of the solder alloys, having been used to assemble the diode.
However the type of solder alloy is selected with taking into account the
properties of the semiconductor. The arsenide diode contain one type of
solders, while the nitride ones contain another.
The importance of laser diode lifetime is understandable for the use in
some CNC machine. It is not so evident for some laser pointer, where the
total working time may be less than a hour during the whole time of its
existence. And here one should remember that along with the operating time
there exists a parameter describing the lifetime "on the shelf". Every
manufacturers does proudly present the operating time of their diode. But
the on shelf lifetime is usually being glossed over modestly. And what
a pity, when three years later, one takes three watt rated "her brilliance"
from the shelf and finds out that it can be addressed only as "mrs. Grey."
Here is an example: two my (not homemade) laser pointers. They aren't
from wicked lasers actually, so don't expect much. I will call them as "the blue one watt rated one" and "the blue two watts rated one", since
their manufacturer and distributor aren't known well.
| Measurement results: |
| |
July 2015 |
January 2018 |
| "the blue one watt rated one" |
650 mW |
576 mW |
| "the blue two watts rated one" |
1160 mW |
710 mW |
The work hours on any of these pointers is in any case less than 10 hours
(and this is an upper estimation with a pretty large margin). The batteries
in both cases were new and freshly charged. The current through the diode
was not measures though, but it is assumed that the driver can support it
on the same and constant level.
I have no such a nice data on the infrared diodes. Two 5-Wt rated diodes
were bought simultaneously in 2014. The first of them was used and finally
burned out, the second one had stayed sealed until the very recent time.
However I can present two numbers: the diode, that was used in 2014, did
3 W at 3.5 Amps, and the other one does 3.2 W at 4.7 Amps now. If we assume
that both diodes were equivalent at the beginning, and if we let the threshold
current be 0.5 Amps, we can conclude that in 2014 they had 1 Wt per Amp, and
now they have only 0.76 Wt per Amp. Not a very precise or reliable data,
but still, the wind blows into the same side as with the laser pointers.
Why should I think that in the observed power reduction the laser diodes
are guilty? One could say that the optics has became dirty (no, it didn't,
it was checked out), or the calibration factor of the laser power meter
has drifted (no, it didn't - checked also) or either the supply current
having been measured that time does not correspond the present one (in
both cases it was measured by new Chinese multimeters.... Maybe the
Chinese have changed the Amp definition?) Also one can say that it is
due the temperature, ambient pressure, humidity, season of the year,
lunar phase....
DOGMA THE SECOND - PRESUMPTION OF DEGRADATION.
What does it mean, degradation? It was already said about the ability of
laser diodes to fail due to every sneeze. And the degradation is the ability
to die step by step EVEN WITHOUT ANY SNEEZE. I.e. during the normal operation
or even during storage on the shelf.
It is considered that the ability to degrade is the main property of laser
diodes. Well... Maybe not exactly the main, but at least the second one after
the ability to emit the light. I hope I don't need to say that I'm kidding
slightly. But every joke contains a bit of truth...
The mechanism of the process is still incomprehensible to me. More common
to deal with elements that have a certain and constant probability of fail.
Like transistors or diodes. If, for example, a new transistor has a probability
of fail ~10% per 3000 hours of work, You can be sure that a used transistor has
the same probability of fail. Exactly for the same reason as the probability
of flipping coin to show the heads is fully independent to how much time
it has shown the heads in the previous flips.
On the other hand the finite lifetime of a laser diode presumes that the
diode contains something expendable or something able to wear out. In order of
nonsense I can suppose that the semiconductor has a non-zero ionic conductivity.
Too small to observe it on the background of the large electron-hole one,
but still there is. As there is an ionic conductivity, consequently there
is an electrolysis. So there are metal dendrites growing from the leads into
the semiconductor volume. Initially they diminish the transparency and finally
cause the complete fail. As I've said it is nonsense, but it is still better
than to consider that there is a finite reserve of electrons and vacancies or
that all the stored inside photons can fly away.
 Return to contents Return to contents
BARS AND ARRAYS
↑

When You feel ready to move towards even higher power, You field of view will
touch some assemblies of multiple laser diodes of certain grade of integrity.
The most widely spread devices of that kind are so called "diode bars" and "diode arrays". They are mainly intended for use for solid state lasers pumping.
Their parameters are also optimized for that task.
From the point of view of using in laser pointers or other devices for laser
cutting the bars and arrays have the next two drawbacks of most importance:
- Their emitting area is too large;
- They require water cooling.
When You consider the size, the output and the bucks per watt independently
to these two factors, You may conclude that usage of laser diode bars and
arrays is very attractive. But think: the typical size of the emitting body
of most bars is about 10 mm long. I.e. when the focal length of Your collimator
of 100 mm (comparatively large value), You will get the divergency of 100 mrad.
It means that at the distance of merely one meter, You will be able to focus
the beam into a stripe shaped spot with the length not less than 100 mm. (Look
to the OPTICS part in the COLLIMATOR
department.) The same thing is with sharp
focusing. Separate laser diodes allow to reach several tens of kilowatts per
square centimeter and to cut, say, a steel. On the contrary with arrays and
bars one will stick to several hundreds of watts per square centimeter and
will be able to cut cardboard and wood only. One may note that such a system
will cut a cardboard in "wholesale volumes" - fast and in large amounts.
However it is most probably not exactly what You want.
One can also do as it is described in the METHODS OF POWER INCREASEMENT BY
ADDING MORE LASER BEAMS TOGETHER part, and try to gather the rays of all
diodelets into one common beam without loosing the brightness. However the
main obstacle on this way will be the main advantage of the bars and arrays -
their compactness. The diodes are so small and placed so tightly, that it
requires to be able to use rasters of microlenses (or micromirrors) to do
something good with the beam.
The paradox is that the separate diodes or sparse assemblies of diodes
(like NUBM08, NUBM44) allow (after geometrical summation) to get more
dense beam (more correctly: more bright beam) than the dense bars
and arrays.
Note: Large emitting body and high divergency are usually not a big problem
when using arrays and bars for pumping a solid state laser. Its laser rod is
big enough and it is close enough to the pump source, so one does not need
to be a marksman to hit the target. However I'd not recommend for an amateur
to build a full scale diode pumped solid state laser. In the best case You
will get the output of only 40% of the sum of the outputs of the diodes used
to pump that laser. And even to get this silly efficiency, You will need to
use a true thermal regulation, not bare heat sink. Note that a full scale
thermal regulation system adds size, weight, cost and consuming power. The
complexity is not the least factor here too. In addition to this You will need
to get rare laser rods and mirrors. The mirrors of random kind wont suit -
they must have proper transmittance and curvature, otherwise its "bye bye power"
again. And finally if You've succeeded with all these obstacles, You may find
that the gain, due to lower divergency of the solid state laser beam, may be
not worth of all the efforts.
Concerning the second drawback - the necessity for water cooling - it is
especially sharp when You are designing a portable system (a device based on
a 100 W rated laser diode bar can hardly be named as "laser pointer"). If a
tabletop CNC laser engraver requires water cooling You won't be happy too.
The fact, that common tap water won't suit, makes things even worse. No,
distilled water won't suit either. It needs a very specially cleaned water
with greatly reduced corrosion activity - so called "deionized water".
Fortunately it is affordable now - one can find it in supermarkets, where
it is being sold for filling irons. However if Your system was not equipped
with a special filter - deionizer, the lifetime of deionized state of water
bill be from several hours to several days. And You will have to replace the
water at the same intervals of time. Or at least have to monitor its state
(by measuring its electrical resistance). Otherwise the water will erode
the microchannel heat exchangers of Your bars and arrays just like sulfuric
acid erodes clothes.
In addition these microchannel heat exchangers use to blind with solid
particles in water. One needs a virulent filtration of water from all
mechanical impurities. A common automotive fuel filter is not enough here.
There also is even a third drawback worth of mention here. Most of laser
diode arrays and bars are packageless. It means that their emitting face
is open for all the surrounding dangers, including dust and dirt. Generally
there exist separate diodes that are packageless too. But in case of separate
diodes one can avoid their usage, because there are plenty of packaged ones.
In case of diode arrays and bars there are usually no alternatives.
Here is a good place to mention:
DOGMA THE THIRD. DOGMA OF PURITY (DON'T DESECRATE YOU SHINE).
Its formula is: IF LASER DIODE IS DEAD AND IN SOME MIRACLOUS WAY THE POWER
UNIT IS INNOCENT, THE GUILT BELONGS TO DIRT.
In practice it means that all operations with packageless laser diodes must
be made in so called "clean zone" only. To understand clearly what does it
mean, go look those advertisement movies about Intel microprocessors, where
guys in spacesuits wander around white shiny rooms.
Think as that. Let we have a laser diode emitting 5 watts of power. The
length of its emitting stripe is about 100 microns. Its height ~1 micron.
Thus those 5 watts are applied to the area of one millionth of a square
centimeter. It gives intensity of 5 MEGAWATTS per square centimeter.
With that intensity any light absorbing matter would explode instantly.
And any dust particle on the emitting surface will explode itself and will
damage the output mirror of the diode. Exactly this way of thoughts leads to
insisting on dealing with laser diodes inside the clean zones exclusively.
On the other hand the area of the emitting face is small and the probability
of the a dust particle to hit this area is similar to the probability of an
asteroid to hit the Earth. It may be expressed in numbers too. From ISO
standarts we know that a general premises with regular wet cleaning has air
with 1e5 to 1e6 particles per cubic meter. I.e. not more than one particle
per cubic centimeter. Assuming that the air moves with a speed of ~1 m/s
(say a light draught) we will get the flux density: 100 particles per square
centimeter each second. By multiplying the flux density by the area of the
emitting face (one millionth of square centimeter) we obtain that the
probability of a particle to land onto the mirror is 1/10000 each second.
In other words the average safe lifetime of the diode in these conditions
is about two hours with a half.
The result of the estimations is that the probability for a diode to fail
due to the dust is rather low, but still considerable. It is understandable
that it is a bad idea to store or use the packageless diodes outside of
vacuum tight laser casing. On the other side if You only pick the diode
out of its tare to install it into the casing of Your laser, and if this
action takes, say, not more than 10 minutes, the probability of the success
is very high. If the air in the room is still, this probability is even
higher.
For the bars and arrays one should take into account that the total emitting
area of all their diodes is much larger, so that the probability of the damage
is much higher too. However it is questionable, whether to consider a bar with
only one fault diode to be faulty or not. If one assumes that a bar is good if
more than 70% of its diodes are good, then the lifetime of the bar in dusty
air will be of the same order as the lifetime of one diode.
 Return to contents Return to contents
MODULES WITH LIGHTGUIDE OR OPTICAL FIBER OUTPUT
↑

There is another pair of types of diode laser products worth to mention here.
These are assemblies of laser diodes having common output equipped with a
lightguide or an optical fiber. In this context a lightguide differs from an
optical fiber mainly by its diameter (and connector type). Lightguides have
their diameters of about a millimeter, and used mainly in powerfull emitters
for laser technologies (welding, cutting, tempering). They transmit powers
of about kilowatt. Optical fibers have typically diameter of ~100 mcm and
intended to transmit lower powers - several tenth of watts. Their main
application is pumping of solid state lasers or fiber lasers.
From the point of view of a DIYer, who designs a "most powerfull laser
pointer in the world" or a cutting head for some CNC machine, such modules
are the very product. The task of geometrical summation of power of multiple
laser diodes have already been solves there. And the solution is done with
professional grade of quality, not at the DIYer level (as described in the
METHODS OF POWER INCREASEMENT BY ADDING MORE LASER BEAMS TOGETHER part).
However for all this ointment there still is a fly or two.
The first thing to know when purchasing such a module is that there is
no mass production device of this kind available on the wide market. The
things we meet at the internet auctions are spare parts of disassembled
laser systems or remnants of closed scientific laboratories. It means that
if You had designed Your device to be compatible with this module, and
if this module have failed for some reason, there will be no replacement.
The probability for You to get another compatible module is almost zero.
A module of another type will force You to redesign all Your device.
Second: most of such modules are being sold without any documentation.
And one just can not establish the proper power supply parameters judging
by its outfit only. Nobody can say how many diodes the manufacturer had
connected in series and how many such strings were stacked in parallel.
The seller is usually unable to answer these questions too. And, finally,
one can not open the module freely without having a clean zone at least
(see dogma the third).
Third: If You've purchaser a module with optical fiber outlet and
you are going to use it in a CNC device to cut a wood, it is better to
discard the output fiber and to replace the output connector with an aperture
an some protective glass. THE PROTECTIVE GLASS MUST BE INSTALLED NOT
IN THE FOCUS OF THE INTERNAL FOCUSING SYSTEM! This upgrade (or downgrade)
should be performed accurately and clean (see dogma the third). If the things
left as is, the output fiber will likely burn out after the contact with
smoke or dust during cutting process. Alternatively one could erect a
vacuum tight collimator head around the fiber output. But in this case
it will most probably end up with burned fiber too.
 Return to contents Return to contents
OPTICS
↑
The part "Optics" contains a digest of the most important and useful
conclusions outcoming from geometrical optics. Those ones that will
be of everyday use in the process of laser pointers design or something
like that. The statements are given with corroborations. Most of them
are simplified, but still strict if being applied to the described class
of objects only. Those who think they are specialists will probably still
find interesting facts, they havent known before. Rookies with their
laziness and horror in sight of mathematical formulas will (hopefully)
be amazed by the simplicity - the part is performed in such a way that
very basic school math is enough. Always remember, that formula is like
a picture - it replaces thousands of words. If You know a number - You
know only one design or only one case/ If You know a formula - You know
them all.
Hard to imagine the practical application, where the natural ray of diode
laser would suit. Maybe the usage as a flashlight or, maybe, for holography.
(However the low coherence of the radiation of laser diodes makes the latter
a bit difficult.)
In all other cases one either needs the laser spot to have minimal possible
size in order to have the highest possible intensity, or either needs a
parallel beam. In order to shape the radiation into the parallel beam, or
in order to focus it, one needs a lens, i.e. optics.
And the very first property to know is that ANY OPTICS BRINGS ITS LOSSES.
Professionals, having access to the fancy lenses with high-tech coatings, got
used to bounce the beam back and forward as many times as they wish. But
DIYer is usually free of this opportunity. And the reason is not in the rarity
of the lenses. The reason is exactly in these additional losses.
The reflection on the border of two media, having different refraction
indices (n1 and n2), when the ray goes at the rectangular angle to the border,
can be expressed with the well known Fresnel formula:
(n2 - n1)^2
R = -------------
(n2 + n1)^2
For example each border between air (n1=1) and glass (n2=1,5) reflects 4%.
And it is the best case, when the surfaces are extremely clean and even.
Any dirt or roughness makes the things worse. One can think that the reflected
light is not lost yet. It seems like it may be useful, for example, the
reflected surface is well aligned. However this is wrong for many reasons.
E.g. lens has a spherical surface and gives divergent (or convergent) reflected
beam. And when we try to focus the radiation its focal spot is far away from
the focal spot of the main beam. Another reason is that it is a bad idea to
let the reflected beam to enter the laser diode. So we just can not align the
surfaces in that way... So any reflection means nothing but losses. And in
its own turn it means that any lens, any prism or glass plate reduce the
power by 8..10%.
Take for example the 5 W diode. After it has been equipped by a collimating
lens it gives only 4.6W. A two-element objective with a protective glass will
cut the power to 3.9 W. And the full scale optical system with the astigmatism
compensation, consisting of two cylindrical lenses, two spherical lenses and
certainly with the protective glass will leave only 3.3 W alive.
Are the things really so bad? At least there is an antireflection coating...
Yes it is there. But not here. The wavelengthes of the most powerful laser
diodes are either outside of the "visible" range or at its borders. And these
borders are not taken into account by developers of the common optics, that
can be found in binoculars, cameras, etc... Occasionally the exclusion from
this rule will be the green diodes. But they will only be interesting when
they reach several watts of power and when their price will quit to cause a
hysterical laugh. And if one uses some optics with antireflection coating
intended for other wavelength (or with decoration coating) it will only cause
even more losses. If there was something like 4% per each border of media,
it can easily reach 10% or more in this case, and even the sole collimator
lens can make Your 5 W rated diode to 4W one. The full scale five-element
optical system will humiliate if to the state of 1.5 W.
The most important conclusions, that follow from the said above are:
- Use the most simple optical schemes. Don't use a mirror to turn a beam
if You can turn Your laser itself. Don't use a periscope to displace
a beam if You can move the laser, and so on...
- Use only optics that has antireflection coating for the wavelength of
Your diode. If You don't have one, You better use "naked" (or "bald")
optics without any coating at all.
Since You will stick to the most simple optical schemes and due to the
low quality of the radiation of those laser diodes, in all cases of
practical importance You can use geometrical optics and school knowledge
base to describe the behaviour of the light in Your systems. Nevertheless
I ought to remind here some laws and relations, usefull for further
comprehension.
 Return to contents Return to contents
A. Lense
↑
Let us consider the lense to be thin enough and let's assume that it
works with so called "paraxial" beams (the beams formed by rays coming
at small angles to the optical axis). A lense can be described by its
optical axis, by its foci and by its optical center. The optical center
is a point on the optical axis and in most cases it is positioned at
the place, where the (thin) body of the lense crosses the optical axis.
The foci belong to the optical axis too, and their positions are
symmetrical in relation to the optical center. In other words: "the right
focal length and the left focal length of a thin lense are equal to each
other, provided that the media to the right from the length and to the left
from the length are the same."
A lense obeys the next four rules:
- A ray, coming through the optical center, does not shift and does not
change its direction. Independently to whether the lense is concave or
convex.

- A ray, that comes through a focus of convex lense, refracts in the lense in
such a way, that it becomes parallel to the optical axis. For concave lense
the things are similar: i.e. if some ray comes as if it is going to pass
through the focus, lying on the opposite side of the lense, the ray refracts
in the lense in such a way that it becomes parallel to the optical axis.

- The third rule is just a second one, but taken in reverse: If the ray
goes parallel to the optical axis, then it will refract in the concave
lens so that it will pass through the focus. Likewise for the convex lense:
if the ray was parallel to the optical axis it will refract in such a way,
that we will think as if it has passed through the focus (the one, which
lies at the same side of lense, where the beam has come from.)

- The next rule is generally the consequence of the previous ones, but the
corroboration of this fact is a bit complicated (takes a lot of auxiliary
drawing and argumentation). For our purposes it is simpler to take it as
a separate rule:
Any beam, consisting of rays parallel to each other (so called "parallel
beam"), even in case it is not parallel to the optical axis, will be
gathered into some point after passing through a convex lense. This point
belongs to a plane orthogonal to the optical axis, and the distance between
the lense and this plane is equal to the focal length of the lense. The
plane itself is called "focal plane of the lense" and plays the role of
locus for gathering points for all parallel beams coming through the lense.
For a concave lense any parallel beam, that have passed through the lense,
will look like it comes from a point source, and this point source belongs
to a plane orthogonal to the optical axis and spaced from the lense by its
focal length:

One should remember that these rules are not exact but approximation.
However it is simpler to consider like they are always fulfilled but with
some deviations. Those deviations are called "aberrations."
That's generally all. Further on You can draw the path of any ray in any
of Your optical system, applying laws of geometry with a help of a compass
and ruler. (Sometimes it may be hard to perform, but it is another question.)
- Particularly You should be able to corroborate that if points of some two
dimensional object do serve as sources of rays, then the rays from each of
these points will be gathered into points of another two dimensional object,
after having been refracted when passing a positive lense. And this new
object will be which is geometrically similar to the original one. I.e. the
lense creates 'image' of the original object.

For negative length the situation is nearly the same, with the only
correction, that there are no actual points in space where the ray gather.
The rays only look like they were gathered in some points beyond the
lense. In this case the image is pure virtual.
The distance A from the lense to the original object, the distance A' from
the lense to the image and the focal length f of the lense are tied together
by the 'thin lense' formulae: 1/f = 1/A + 1/A'.
Here we have assumed, that if the distance A' between the lense and the
image is positive, it means the image is real. And if the distance A'
appears to be negative, the image is virtual.
Be attentive, in some textbooks on optics they use another assumption: If
the sign of the distance is positive it means that the image is to the right
from the lense, and the negative sign means the image is to the left. With
this convention the thin lense formulae will look different.
- The value inverse to the focal length, that stands in the left part of the
thin lense formulae is called as "dioptrical" (or simply optical) strength.
If the lense is made of some transparent material, having its refraction
index equal to n, and if it is bounded by spherical surfaces, having their
radii equal to r1 and r2, then the optical strength of the lense may be
expressed as:
1/f = (n/n0-1)(1/r1+1/r2)
where n0 is the refractive index of the surrounding medium. If the
surrounding medium is air it is reasonable to assume that n0=1.
The radius is counted as positive if the surface is convex and it is treated
as negative if the surface is concave.
One may note that the right part of the expression can be written as sum:
1/f = (n/n0-1)(1/r1)+(n/n0-1)(1/r2)
It is just a sum of optical strengthes of two lenses: the first is plano-curved, with the radius of curvature r1, and the second is plano-curved with
the radius of curvature r2. It means that the lense with both curved sides
may be treated as two "plano-curved" lenses, having been put together close
to each other.
- Actually there exists more general statement: two thin lenses of any kind,
when having been put together next to each other, may be considered as one
lense, with its optical strength, equal to the sum of optical strengthes of
its components.
Focal length f and corresponding optical strength 1/f are considered to be
positive for collecting lense and negative for divergent one.
If refractive index of the lense is higher than the one of the surroundings,
than collecting lense will always be convex one (or the one, which is "more
convex than concave", for convex-concave lenses). And similarly some
concave lense (or "more concave than convex") will be divergent.
- There exist yet another interesting understanding of the thin lense formulae.
It can be illustrated by the next picture:

Namely: the lense, that collects rays coming from an object, being placed at
a distance A from the lense, into an image, being at a distance A' from the
lense , can be treated as two lenses: the firs one has its focal length A
and makes the divergent beam to be parallel, and the next lense has its
focal length A' and transforms the parallel beam into the convergent one,
which collects in the correspondent focus (at the distance A').
 Return to contents Return to contents
B. Mirror
↑
"A thin mirror" is very similar to thin lense. One may apply the same
formulas and methods of rays construction. One needs only to keep in mind,
that the reflected ray goes in reverse direction and that the optical
strength of the mirror will be expressed by the formulae:
1/f = 2/r, where r is the radius of curvature of the mirror surface. Neither
the refractive index of material of the mirror, nor the radius of curvature
of the back surface of the mirror do affect the focal length for obvious
reasons.
The reverse direction of the reflected rays makes some difficulties in
the process of their drawing. In some cases it is more robust to consider
the thin mirror as being like thin lense with keeping in mind that in the
real system the rays having been refracted during construction will become
reflected ones with the correspondent change of the direction.
 Return to contents Return to contents
C. The Divergency
↑
It is easy to understand, that by installing a lense into the laser beam,
one can force the beam to diverge or converge. But the term "divergency"
means another thing. The divergency, having been caused by a lense, may
be canceled with another lense. The part of divergency, that can be removed
by a lense, is called "white divergency". But more commonly it just stays
apart of consideration, because it is trivial.
The other part of the divergency, that can not be canceled with any lense,
is called "grey divergency" or simply: "divergency."
Let, for example, the beam consists of several partial parallel beams, going
at small angles to each other. (These partial beams may, for example, be
related to different modes of laser cavity.) If the angles between the
partial beams are small enough, a person, who looks at the whole beam from
some distance, may perceive the whole beam as being almost parallel. However
if one takes a lense and collects the beam, it will be gathered not into a
single point, but into a spot, having finite and definite size:

If the maximal angle between some partial ray and the axis of the whole beam
is alfa, and the focal length of the lense is f, then the radius of the
resulting focal spot will be f*tg(alfa). Or, if we remember that for small
angles tg(alfa)~~alfa (where alfa is expressed in radians), we can say that
the radius of the focal spot is f*alfa.
If the whole beam has axial symmetry, then alfa (the maximal angle between
partial ray and the axis) corresponds to HALF of the divergency. So the
DIAMETER of the focal spot will be f*(2*alfa), where 2*alfa - is the FULL
divergency angle (again for small enough alfa's).
By reading this picture from the right to the left one can note, that
light source, having its diameter delta was placed into the focal plane of
the lense, it will produce a beam with divergency delta/f (in radians). The
outcome of this statements we'll see further on in the part "Collimator".
Now and here let's discuss another case of practical importance. It is
related to the question: "How to measure the divergency?". Indeed, a beam
has unknown white divergency and grey divergency. And we can not just estate,
that the (grey) divergency is equal to the focal spot diameter divided by
the focal length. Just because we have no warranties that the beam will have
its narrowest section at the focal plane and therefore the focal length is
not essential here. Lets investigate this case in more details.
Let for example a beam low (weakly) divergent rays is being collected by a
lense. In other words: the lense is placed into the beam, having white and
grey divergences simultaneously. If the beam is really being focused to
some extent (i.e. if the beam behind the lense becomes narrower and narrower
up to some place, where it has the narrowest section, and only then it
begins to become wider and wider), then we can act exactly like we did in
the section 8 of the part "LENSE". Namely we can imagine that the lense
consists of two parts: the first part cancels the white divergency and the
second part gathers the quasi-parallel beam, that has only grey divergency:

It is now clear, that the divergency of the beam may be determined (in
radians) as the size of the most narrow section of the beam divided by the
distance between the lense and that most narrow section. This distance is
designated as "A" at the picture above.
Indeed, by reading the picture from the right to the left we can see that
the beam without white divergency (the one that goes between the partial
lenses) is formed by the rightmost partial lense from the rays emitted (as
if it was so) by some source having finite dimensions. Moreover one can
consider any section of the beam as this source. Dependently to which
section of the beam was taken as the source the corresponding value of the
divergency cold be equal to a/A, where "a" is the size of the
correspondent section and A is the distance between this section to the
lense. However we are looking for the kind of divergency that can not be
cancelled by any lense. So from the whole plurality of the possible
sections we must choose the one, that yields the lowest possible value of
a/A.
The simplified corroboration may look like this. Let the beam to have
almost conical shape:

If we take the coordinate system, like the one, drawn on the picture above
(the origin is in the narrowest place of the beam), the equation of the
border line of the cone will look like this: y(z) = a + k|z|, where k - is
the slope ratio of the line. Its numeric value will be of low importance
here.
The half divergency angle will then be determined as:
y(z) a+k|z|
min (-----) = min (--------)
z A+z z A+z
By taking the derivative of the function, that stands under the minimum
sign one can see that it has no zeros, and the sole singularity takes place
at the point z=0. It means that if the original has a minimum, it is reached
exactly at the point z=0. So under the current assumptions the (minimal or
grey) divergency is equal to the size of the most narrow section of the beam
divided by the distance between this section and the lense.
The only assumption required is the conical-like shape of the beam. It
means that the statement is valid if the conical shape describes the
(longitudinal) shape of the beam good. In other words the focusing should
be sharp enough. Yet in another words: the length of the caustic of the
focused beam should be much less than the distance between the lense and
the most narrow section of the beam.
 Return to contents Return to contents
C. The Caustic
↑
From the said above one can see that a real beam, having some finite
divergency, is focused by a lense not into exact point, but into some spot
with finite dimensions. It means that near the most narrow section of the
beam one can select an (imaginary) area, where the size of the beam section
varies insufficiently. This area is called "beam's caustic".
Some ambiguity lies in the definition of how strong can the size of the
beam vary, while we still can consider those variations as small enough. If
You let the tolerance go towards zero, the length of the correspondent
caustic will also converge to zero. Independently to how fast the beam does
converge or diverge and independently to the focal spot size. And vice versa
if we let the tolerance to be large enough, we can consider the whole beam
as caustic. A simple and reasonable assumption is to define caustic as such
a zone, where the ideal beam (the one without any grey divergency) has its
size equal or less to the minimal size of the real beam when focused by the
same lense:

For the real beam it will correspond to the area, where the current size
(diameter) of the beam does exceed its minimal size not more than twice.
From the picture above, using the similarity of the triangles one can see
that:
Lc/2 A A
------- = ---- => Lc = 2*delta*---
delta/2 Do/2 Do
With such a definition of the caustic length Lc the intensity of the light
on the beam axis varies by four times along the caustic. Indeed: the diameter
of the beam doubles from the center of the caustic to its end. It means the
area of section grows by the factor of four. The power of the beam is,
obviously, constant, so the intensity (like the ratio of the light power to
the area of the beam cross section) varies by the factor of four, just like
the area does.
One can define the caustic as a zone twice as short as it was in the
considerations above. Then the bothersome "two" will vanish from the
formulas, and: Lc = delta*A/Do. The growth of the beam diameter (from the
center of the caustic to the end of the caustic) will now be 1.5 times. And
the intensity in that caustic will vary only in the limit of (1.5)^2 = 2.25 ~~ 2.
The variation of the intensity in the limits of two does affect the
"drilling-cutting" properties of the beam much less, so further on we will
use this definition of the caustic.
The minimal beam diameter in the caustic will be delta = alfa*A = alfa*D*(A/Do).
While looking at the picture one can note that Do/2A is the tangent of
the half angle of the convergence of partial rays. In the approximation of
small angles, the tangents and sinuses of the angles are equal to the
original angles in radians. If we define Do/A as gamma - the angle of the
beam convergence, then we can estate, that the minimal size of the beam in
its caustic is reversely proportional to the gamma:
delta - alfa*Do*(Ao/Do) = alfa*Do/gamma.
I.e. more sharp focusing yields narrower spot. Obvious result, isnt it?
The angular divergency of the beam is generally not independent
parameter. On the contrary, one can use various optical systems to change it
to the desired value. Further on (see parts "collimator" and "telescope")
it will be shown that the angular divergency of the beam is reversely
proportional to its diameter: alfa ~ 1/Do or alfa = k/Do, where k is a
factor, that depends only to initial conditions.
Finally: delta = alfa*Do/gamma = (k/Do)*Do/gamma = k/gamma.
It appears that the minimal beam diameter is inversely proportional
to the angle of convergence of the beam. This angle is called "angular
aperture".
 Return to contents Return to contents
D. Collimator
↑
The term "collimator" is reserved for designating a device intended for
obtaining some parallel beam of something. This "something" may be light,
or electrons, or protons or either any kind of matter. We will discuss
a simplest form of light collimator, that consists of a single lense. As
it literally follows from the second rule of thin lense: if there exists
a point-like light source and if it was placed into one of foci of some
lense, the lense will collect all the rays coming from this point-like
source into a parallel beam of light, that goes along the optical axis.
The real source of light has finite size delta and emits beam of light
having finite divergency alfa. If such a source was placed to focal plane
of a positive lense with focal length f, the rays after having been
refracted in the lense will form the beam with a new value of divergency:
alfa'= delta/f.
One needs keep in mind that for this to be true, the size of the source
delta has to be small enough for the condition alfa'<alfa was fulfilled.
Otherwise an embarrassment may occur, like it is shown on the next picture:

On the picture above the condition alfa'<alfa is not satisfied and the
beam in the focal plane of the lense has smaller size than it has in the
plane of image. I.e.:
When the size of the source is small and the divergency of its radiation
is high, the divergency of the beam after the lense depends mostly to the
size of the source (and obviously to the focal length of the lense).
However when the size of the source is large but the divergency of its
radiation is small, exactly this divergency becomes the determining one.
Particularly this situation is usual for common lasers: when for example
a ruby rod has diameter like 1 cm and the divergency of its radiation
is something like 1 mrad. In this case the diameter of the caustic is
defined not by the size of the source but by the divergency of the beam.
Moreover the beam itself may be considered as one carrying an information
about some virtual source, very small and very far away. The size of this
virtual source and the distance to it may be calculated using the already
known to us rules.
Lets return to the case of using a collimator lense, when the size of
the source is small enough. In this case (as it has already been said above)
the size of the source completely defines the divergency of the beam after
the collimator: alfa' = delta/f. The initial divergency alfa is only
essential to determine the size of the lense necessary to gather all the
light into the collimated beam.
Generally nothing forbids to take a smaller lense, the divergency of the
resulting beam won't depend to this. But the power will.
Example (A): pocket flashlight lamp has its incandescent filament with
its length of 3 mm. It means that it is enough to take a lense with focal
length of 3 meters in order to achieve "laser-like" divergency of 1 mrad.
Let the diameter of this lense be 100 mm. Taking into account that the lamp
light goes into all directions uniformly, we can calculate the area of
surface of a sphere, being crossed by the light at a distance of 3 meters
from the lamp: 4*pi*R^2 = 1.1 mln of square centimeters. Our lense covers
the area of only 78 square centimeters. It means that only 0.007% of the
light, emitted by the lamp, is being caught by the lense and used to form
the collimated beam.
Example(B): A laser diode, having the width of the emitting stripe of
100 mcm. With the fast axis divergency 60 degrees and slow axis divergency
of 10 degrees. In order to achieve resulting 1 mrad of divergency one needs
to choose a focal length of 100 mm. At these 100 mm the frustum of light
from the laser diode will have its section in the shape of a stripe 17.5 mm
wide and 115 mm long. If using a lense 100 mm in diameter we could gather
87% of the light into collimated beam having its divergency at the level
of 1 mrad in its fast axis and even lower in the slow one. However here
are some difficulties.
First: due to the fact that the lens having its diameter of 100 mm is
lit by a strip of light 18x115 mm, most of the lense area is just out of
the job.
Second: We assume that the lense has too mm focal length and 100 mm
diameter. Remember the formulae for the optical strength:
1/f = (n/n0)(1/r1+1/r2)
where r1 - the radius of curvature of the first (convex) surface,
bordering the lense;
r2 - the radius of curvature of the second (convex) surface;
n0 - refractive index of the surroundings;
n - refractive index of the lense material;
f - the focal length.
For the simplicity lets assume that r2=infinity (plano-convex lense),
n0=1 (air) and n = 1.5 (common glass):
1/f = (n-1)(1/r1) => r1 = (n-1)*f ~~ 0.5*f
I.e. if we require the diameter of the lense to be equal to its focal
length the lense will become a hemisphere. It is easy to get that the focal
length of a ball of common glass is equal to half of its diameter, i.e.
equal to its radius. And it is the limit. One can not make the focal
length to be even shorter when the diameter of the lense is constant.
Exactly this property determines that the more optical strength the less
is the lense diameter. In the application to the current example it means
that one requires a lens that has a shape of hemisphere and moreover -
80% of its surface is useless. The collecting properties of such a lense
would be far from ideal and the divergency of the resulting beam would
be mostly determined by the aberrations.
Example (C): Exactly the same laser diode like in the previous example,
but having a FAC lense on it. Let the diameter of the FAC lense
(cylindrical) body be 100 mcm and let's take that it compensates the
fast axis divergency towards the same 10 degrees.
In this case at a distance of 100 mm from the laser diode the spot will
be 17.5 x 17.5 mm and one can fully cover it with a 25 mm lense. For the
size of the light source we can take the size of the FAC lense area, lit
by the light of the diode: 100 mcm x 100 mcm. So we can see that in order
to obtain 1 mrad rated beam we can use lense with 25 mm diameter and
FL = 100mm.
Example(D): Lets take a light source with its size delta and divergency
alfa and install it into focal plane of a lense, having its focal length f.
If we can neglect the size delta in comparison with alfa*f value, then the
beam diameter on the lense surface will be alfa*f and the divergency after
the lense will be delta/f.

Lets look at the grade of divergency diminishing, i.e. let's consider the
alfa'/alfa ratio:
alfa' delta/f delta
----- = ------- = ------
alfa alfa alfa*f
Note that alfa*f expresses the size of the beam on the surface of the lense.
It means that the ratio of the divergency after the lense to the initial
divergency is equal to the ratio of the size of the source to the size of the
beam spot on the lense.
In other words the divergency diminishes as much times as the size of the
beam becomes larger.
Yet another terms: the linear magnification is in reverse to the angular
magnification.
If one considers the same problem in 3-dimensional space and in when
referenced rated to the cross sectional area of the beam, one can come to
even more general conclusion: if the losses are negligible the
brightness of the beam after collimator is equal to the brightness of the
light source.
Using this rule one can immediately (without any intermediate computations)
say that the lesser we want divergency to be, the larger optics we will need.
In the reality divergency itself is a value of rather low interest. Usually
we need intensity - laser beam power divided by its cross sectional area. So
we are usually interested in size of laser spot.
From the pictures above it is obvious that a beam, having its initial
diameter of alfa*f on the lense, does grow further on as alfa'*z, where z is
the distance between the lense and the point of interest. I.e. diameter of
the collimated beam behaves like: Dc = alfa*f + alfa'*z. In such cases, when
alfa'*z >> alfa*f = Dc(z=0) /in so called "far field zone"/ the area of the
laser spot is completely determined by the divergency and nothing could be
done. But in such cases, when the initial beam diameter Dc(z=0) is comparable
or greater than the enlargement of the beam due to its divergency, we can
cancel that initial beam diameter just by focusing.
Suppose we need to focus the beam to the spot at the known distance L from
the collimator. Let's install a lens with focal length equal to L immediately
after the collimator:

As we already know, two lenses close to each other may be considered a one
lense with its optical strength equal to sum of optical strengthes of the
original lenses, It is evident, that in our case the total optical strength
will be greater than the optical strength of the initial collimator. Since
that the focal length will become shorter, and the source will appear to be
placed not exactly into the focal plane, but at some distance, which is
greater than the focal length of the new lense.
Going further we can note, that in order to focus the beam into a certain
place one does not need to actually add some new lense to the collimator. One
just needs to move the lense farther apart from the source. The new distance
will then be L*f/(L-f). (One may notice, that for any positive values of L
this distance is greater than the focal length of the lens being in use.)
The spot size delta' will then be equal to the angular divergency
multiplied by the distance between the lense and the spot. (If angles are not
small enough and You can not neglect the difference of tg(alfa') from the
alfa', You will need to multiply the distance not by the angle itself but
by doubled tangent of half divergency angle. The formulae will become more
complicated but generally the result behaves similarly.) The angular
divergency in its own turn will be equal to the source size delta divided
by the distance to the lense:
delta delta*(L-f)
delta' = L * ----------- = ----------- = delta*(L/f-1)
L*f/(L-f)
From here it is clear, for example, that at large distances, when L/f>>1,
the spot size may be expressed as delta' = delta*L/f. I.e. to obtain small
spots at large distances one has to use lenses with long focal lengthes.
One may come from another side too: let's multiply the nominator and
denominator by the source divergency alfa:
delta * alfa L*delta*alfa
delta' = L * -------------- = ------------
L*f/(L-f)*alfa Do
...and notice that denominator contains the source divergency multiplied
by the distance from the source to the lense, i.e. the beam diameter on the
lense surface Do, resulting to the conclusion that:
At given source parameters (size and divergency) the minimal possible
spot size at given distance l is reversely proportional to the diameter of
the working (occupied by light) area of the lense.
Simply speaking the range of Your laser pointer action is proportional
to the diameter (aperture) of Your optics.
At the end of our analysis of collimator, we must mention another
important case: collimator with fast axis compensation lense.
If we look at the problem in the plane of slow axis, it has negligible
difference from the already discussed case of the single lense collimator.

Small shifting of the rays on a small plano-parallel glass object may
be easily neglected.
And if we look at the problem in the plane of fast axis, where the
cylindrical FAC lense has considerable optical strength, we have now a
two-lensed system and its consideration precedes the discussion of a
telescope (see further in the part entitled "telescope"):

It was said above that in principle the area of the cylindrical lense lit
by light of the diode can be treated as a small light source of known size.
This approach is good if the lense is small (e.g. the internal FAC lense of
the diode). On the contrary if the lense is large (maybe You are using a
5 mm glass rod to correct the beam) this approach becomes too rude. It still
works, but one can get better results, than those, You get when tuning the
collimator to translate the image taken from the lense rather than taking
from the diode itself.
On the other hand, the results one can get, when the collimator is tuned
for taken image from the diode, depend strongly to how the FAC lense is
actually installed. For example if it is tuned for full compensation (for
parallel beam), any kind of spherical lense installation will only lead to
that the rays will just be gathered in its focus. And due to the fact that
the caustic of the beam in the slow axis plane will almost always be far
away from the focus of the lens we will result in distorted beam with low
intensity. It is clear now, that full compensation is not profitable. And
the question is: what kind of FAC lense setup is most profitable?
We saw above that the achievable minimal spot size is usually smaller
for larger size of the laser beam cross section on the focusing lense.
It means that a good choice for the position of the FAC lense will be
the one, that provides the best filling of the focusing lense with the
light. Typically lenses have square or circle-like shape. It means that
both sizes of the beam (the one along the fast axis and the one along
slow axis) should be equal to each other. That is why at the picture above
it was noted that alfa_x=alfa_y.
It means that the fast axis compensation lense is profitable to be
installed in such a position that the beam would continue to diverge after
it. (And this divergency would be of the same order of magnitude with the
divergency over the slow axis.)
Let's see how it affects the work of the collimator.
Let the initial divergency of the radiation from the source over the fast
axis be alfa_y_0. Let the cylindrical lense to have its focal length fc, and
it is installed in such a position, that the white divergency of the rays
after the lense is alfa_y. Then the output lense "sees" the rays as if they
were emitted not by the source, but by its (virtual) image.
Using the thin lense formulae and making corroborations a bit more
complicated, than desirable for being presented here, one can obtain, that
the mentioned virtual image of the source is placed slightly more far away
from the output lense than the source itself. And the shifting S (the
distance between the real source ant its virtual image) is equal to:
S = fc * (alfa_y/alfa_y_0 + alfa_y_0/alfa_y -2)
And the source must be placed at an exact distance A from the
cylindrical lense:
A = fc * (1 - alfa_y/alfa)
Thus, if we set the output lense in such a position, that in the slow
axis plane the source appears to be in the focus of the lense (or in the
plane of sharp imaging), then in the fast axis plane the source behaves like
being behind the focus with the shifting of S. And vice versa - if we tune
our output lense for the sharp focusing in the fast axis plane, then in the
slow axis plane the source appears to be shifted by S forward against the
position of exact focusing. You can see that in any case the "tuning to the
acuteness" appears to be broken. What can be done here?
The first thing, coming to the brains is to add a cylindrical lense to
the output spherical one. And this new cylindrical lense should have its
optical strength exactly equal to one needed to compensate the mentioned
shift of the image. This procedure is sometimes called "to compensate the
astigmatism". However cylindrical lenses are rare and it is quite difficult
to get a cylindrical lense with the needed size and curvature. Moreover this
method contradicts the principle (given at the very beginning of the part
entitled "Optics") that recommends not to add excessive lenses and surfaces.
So what can be done again?
It appears that one could tilt the lense. And just in accordance with
the rules of geometrical projections its focal length and radius of
curvature as seen by the light, coming along its previous optical axis,
would shrink by cosine of tilt angle times.

This statement can be corroborated more seriously: by calculation of
optical path difference for different rays and then by relating this
difference with the distance between these rays, i.e. by means of wavefront
camber calculation.
One should note, that this statement is in awkward contradiction with the
fourth rule of thin lense. However the rules of lens are idealization, and
the property of the tilt lense to have different focal lenghtes for the
beams of rays lying in different planes is the correction for this
idealization. This correction is one of aberrations and it has the name "astigmatism".
The angle and direction of the lense tilt may be chosen in such a way,
that in the plane of slow axis the source itself was in the focus of the
tilt lense, and in the plane of fast axis the virtual image of the source
was in the focus too. This situation is shown on the picture below:

NUMERIC EXAMPLE:
Suppose we have a diode with 60 degrees divergency along its fast axis and
10 degrees along its slow axis. Then by means of a cylindrical lense with focal
length 3 mm both (white) divergences are made to be equal to each other. For
the further transformation of the radiation into the (quasi) parallel beam
we are forced to use spherical lense with focal length 100 mm. Determine the
needed lense tilt angle.
SOLUTION: in our designations alfa_y_0 = 60 degrees, alfa_y = alfa_x = 10
degrees, fc = 3mm, A = 100 mm.
Calculating the coordinate difference between position of the source and
position of its virtual image given by the cylindrical lense:
S = fc * (alfa_y/alfa_y_0 + alfa_y_0/alfa_y -1) = 3*(6+1/6-2) ~~ 12 mm.
The maximal focal length of the tilt lense is f, and the minimal one is
f*cos(theta), where theta is the lense tilt angle. Thus the difference
between focal lengthes is f - f*cos(theta) = f*(1-cos(theta)).
For the acute imaging this difference should be equal to the coordinate
difference between the source and its image. This value was calculated above
and designated as S.
f*(1-cos(theta)) = S => 1-cos(theta) = S/f => cos(theta) = 1 - S/f
Substitute there S=12 mm and f=100 mm:
cos(theta) = 1-0.12 = 0.88 => theta = 28 degrees.
One can see that this example requires serious tilt. At such a high values
of tilt there may appear not astigmatism only, but other aberrations too.
In order to avoid this one should choose smaller values of tilt. It may be
done by choosing the cylindrical lense with shorter focal length. Here is a
good place to note, that focal length of 3 mm corresponds to cylindrical
lense, made of a 4 mm bore glass tubing filled by water.
ANOTHER EXAMPLE:
Suppose all initial data are exactly the same as in the previous example.
With the sole difference that the cylindrical lense has focal length of
120 mcm - i.e. the diode is supplied with the internal FAC lense.
SOLUTION:
S = fc * (alfa_y/alfa_y_0 +alfa_y_0/alfa_y -2) = 0.12*(6+1/6-2)~~0.5 mm.
cos(theta) = 1-S/f = 1-0.5/100 = 0.995 => theta =5.7 degrees
Here is the reverse situation: the tilt is small and in rough DIY designs
it may appear to be less than the angular errors of lense position.
COLLIMATOR DESIGN EXAMPLE:
A collimator uses a (spherical) lense with focal length of 100 mm. Find
the required range of position of the lense relatively to the source if the
minimal distance for the beam to be focused is Lmin=0.7 meter and the
maximal distance for the beam to be focused is Lmax=5meter. Find also the
required size of the lense, assuming that the opening of the directional
characteristic of the diode is equal for both axes and equal to
alfa = 10 degrees.
SOLUTION:
Use thin lense formula twice:
1 1 1 1 1 1
--- = ---- + ---- and --- = ---- + ----
f Amax Lmin f Amin Lmax
Here Amin and Amax are the values to be found, namely minimal and maximal
distance from the lense to the diode.
Substituting numbers: f=100 mm, Lmin = 700 mm, Lmax = 5000 mm and using
some calculator we get:
Amax = 116 mm, Amin = 102 mm.
At 116 mm from the diode its beam cross section will have square shape with
the side of Amax*2*tg(alfa/2) = 17 mm . If the lense is round, this square
has to be inscribed into some circle with its radius to be found. If side of
square is a, then radius of circumscribed circle is a/sqrt(2). So the sought
radius is 12.4 mm. And the necessary lense diameter is ~25mm.
FURTHER EXAMPLE:
In the conditions of the previous example, find the sizes of laser spot at
minimal and maximal operation distances, taking a lit part of the FAC lense as
the light emitting body. Let this lit part to have size 100 x 220 mcm. Also
find the intensities in the laser spots at both distances, with knowing
that the diode emitted power is W=5W.
SOLUTION:

Use the first rule of thin lense and note, that the triangles, formed by
border rays and having common vertex at the optical center of the lense, are
similar. You will get then:
Dx = (L/l)*d_x ; D_y = (L/l)*d_y
Where D_x, D_y - the sizes of the image along the correspondent coordinates,
d_x = 220 mcm, d_y = 100 mcm - the sizes of the source along the same
coordinates.
Note also, that for the case of focusing to the minimum distance:
L = Lmin = 700 mm (from the previous example), l = Amax = 116 mm.
For the case of focusing to the maximal distance:
L = Lmax = 5000 mm (again from the previous example), l = Amin = 102 mm
Using a calculator one can get:
D_x(700mm) = 1.3 mm ; D_y(700mm) = 0.6 mm;
D_x(5000mm) = 10.7 mm; D_y(5000mm) = 4.9 mm
The intensity I will be expressed as the diode power divided by the spot
area: I = W/(D_x*D_y)
I(700 mm) = 641 Wt/sq.cm.
I(5000 mm) = 9.5 Wt/sq.cm.
The first is more than enough to cut through a wood, and the second is
barely enough to lit a match.
 Return to contents Return to contents
E. Telescope
↑
Telescope is a system, consisting of two lenses, spaced from each other by
a distance, nearly equal to the sum of focal lengthes of these lenses. Among
the whole bunch of telescope types we will discuss only lensed types, and will
divide the latter into two big classes:
Keplerian telescopes - consisting of two collecting lenses;
and
Galilean telescopes - containing one diverging lense.

If we assume that focal length of a diverging lense is negative, the
definition above suits both types of telescopes.
If the distance between lenses in telescope is exactly equal to the sum of
their focal lengthes, they say that telescope is "tuned for the infinity".
Using the second and third rules of thin lense, it is easy to get, that if
some parallel beam enters some "tuned to the infinity" telescope parallel
to its optical axis (parallel to the line that connects optical centers of
lenses), then the exit beam will also consist of parallel rays.
It is also simple to deduce that diameter of the entering beam D1 and
diameter of the exiting beam D2 are related to each other as the ratio of
(absolute values) of the focal lengthes of correspondent lenses:
D2/D1 = |f2|/|f1|.
In order to do this for a telescope, consisting of only collecting lenses,
one needs only to draw the path of bordering rays:

And to note the similarity of the triangles, having the common vertex at the
point of coincident foci of the lenses. (The basements of those triangles
are the lenses themselves, if considered as geometrical lines.)
For Galilean telescope the consideration would be fully analogous. One need
only to remember the third rule of thin lense and to continue the lines
(rays) to a point behind the negative lense, from where those rays are
virtually emitted:

The said shows that the first property (and application) of telescope is to
transform beam of one diameter into a beam of another diameter.
Need to notice, that when constructing a telescope in practice, nothing
really forbids to take the output lense smaller than it yields from
the D2=D1*|f2|/|f1| relation. Some light will be just lost. All other functions
of the telescope will stay intact.
Lets discuss the path of rays in the "tuned to the infinity" telescope again.
However let's now apply some finite divergency alfa1 to the incoming beam.
(Strictly speaking for the further considerations it is of no importance
whether this divergency is of white or grey type.)

As it had already been shown above, a lense, having focal length f, will
gather this beam into a spot with diameter delta = alfa1*f1. The spot under
consideration is in the focal plane of the first lense. Somewhere else there
may be a smaller spot, but it is of no importance, because the next step is
to take this spot as a light source being in the focal plane of the second
lense. Such a problem has also been discussed above and the result is that
the exiting beam will have the divergency of alfa2 = delta/f2.
I.e. the ratio of the angular divergency of the exiting beam alfa2 to the
angular divergency of the entering beam alfa1 will be equal to the ratio of
the focal length of the entrance lense f1 to the focal length of the exit
lense f2:
alfa2/alfa1 = |f1|/f2|
The alfa2/alfa1 ratio is called as "angular magnification" of the telescope.
The angular magnification in the geometrical optics is generally untied with
the ratio of diameters of the lenses. However if the output lense is smaller
than a certain size, some part of light would be lost.
Moreover, as one can see at the picture above, when we telescope a
diverging beam of rays, the needed ratio of the diameters of the lenses is
not exactly equal to the ratio of their focal distances. The foregoing
approximative expression is more applicable here:
D2~~D1*|f2/f1|+alfa1*(f1+f2)
Only in case when alfa1 is small enough to neglect the second member of
the expression, one may say that D2/D1 = |f2/f1| = alfa1/alfa2.
I.e.: "The value, how much the diameter of the beam was increased, is
equal to the value of how much the divergency of the beam was diminished".
Or else: "angular magnification is in reverse proportion to the linear
magnification."
For the Galilean type telescope things are generally the same. One needs
only to take into account, that the rays go after the diverging lense as if
they were emitted from (a virtual) image, positioned at |f1| to the left from
the lens.

By using the first rule of thin lens one may find that the linear size
of the virtual image will be delta=|f1|*alfa1, and thus the divergency
after the refraction in the output lens will be: alfa2=alfa1*|f1|/|f2|
In the approximative formula for the necessary lens diameter one should
keep in mind the sign of focal length and take care for the diameter to
be positive:
D2~~D1*|f2/f1|+alfa1*(f1+f2).
If written in absolute values:
D2~~D1*|f2|/|f1|+alfa1*(|f2|-|f1|).
In this form it is more clear that the correction value for the necessary
diameter of the output lens is lesser than in the Keplerian telescope. It is
due to the fact that the tube itself is shorter. (The distance between the
lenses is here equal not to the sum of two positive focal lengthes but to the
sum of the positive focal length of the output lens and negative focal length
of the diverging lens.)
By the way one can note that if Keplerian telescope is able to be tuned for
the infinity in any case, Galilean one can be tuned to the infinity only if
the absolute value focal length of the diverging lens is smaller than the focal
length of the gathering lens.
Its time to discuss a telescope having been tuned out of the infinity
position. Imagine we have a telescope consisting of two lenses with focal
lengthes of f1 and f2. Let these lenses are placed so that there is some
spacing X between their foci. And finally let this spacing be positive: X>0.
I.e. lenses are spaced one from another by some distance greater than the
sum of both focal lengthes. As shown on the next picture.

Lets put a beam of parallel rays to the entrance of the telescope. Obviously
it will be gathered into the focus of the first lens. I.e. at the distance of
f1 from the lens. This point may be considered as a source of light for the
next lense. And this source is placed more far from the lense than its focus:
f2+X >f2. As we already know, if the source is placed more far from (positive)
lense than its focus, the lens will gather the rays into some real image.
For the point-like source the image will be a point and its position can be
found using the thin lens formulae. The distance from the telescope to that
image we will determine a bit later. Now lets note another interesting fact:
as the image appears to be a single point it means that the beam of rays
appears to converge. I.e. if distance between lenses of telescope is greater
than the sum of their focal lengthes, the telescope will always transform
any incoming parallel beam into some converging one.
On the contrary if distance between lenses of a telescope is smaller than
the sum of focal lengthes of the lenses, the telescope will transform any
incoming parallel beam into some diverging one.

One can prove it similarly: trace the path of the rays and note that after
using the thin lense formulae You get negative distance from the lens to
the image. I.e. the image is pure virtual and has form of a virtual point to
the left from the lense. The rays go as if they've been emitted from this
virtual point.
It means that by means of changing the distance between lenses in telescope
one can make the telescope to converge the beam or to diverge by will. In
other words the telescope behaves like a lens with variable focal length.
Such an application is very robust. If You need to focus a laser beam onto
an object, placed at, say, 47 meters from the laser, You do not have to
rush in a search for a lens with 47 meters focal length. Just get a telescope
(half of some binoculars or whatever), let the beam to pass through it, and
using its focusing control, focus the beam to the target at almost any desired
distance.
"Why almost?" - At least it is obvious that at any case the minimal distance
of focusing can not be shorter than the focal length of the output lens. In a
real telescope the minimal achievable distance of sharp focusing will be
determined not by the focal lengthes only, but also by the limits of motion
of lenses.
Lets discuss such an application in more details. Imagine there is a light
source with its size designated as delta and consider it emits a beam of rays
with angular divergency alfa1. Assume the source is at a distance of L1 from the
entrance lens of the telescope. Let's use the telescope to focus the beam into
a spot at a distance of L2 from the output lens. The word "to focus" means here "to obtain the minimum possible spot size." However we've already seen that the "minimum possible size" may be determined either by the size of the image of
the source or by the divergency of the rays. Let's take that the divergency is
comparatively high and the minimum of the size is determined by the size of the
image only.

- At the entrance lens the beam from the delta1 sized source having the
divergency alfa1 forms a spot with the size of
D1 = delta1 + L1*2*tg(alfa1/2) ~~ delta1 + L1*alfa1.
- At A1 from the entrance lens there appears an image of the source. The
image (real one for Keplerian telescope and virtual one for Galilean one) has
the size of delta2 = delta1*(A1/L1). The value of L2 may be evaluated using the
thin lense formulae:
f1*L1
A1 = --------
L1 - f1
from here:
f1
delta2 = delta1*-----
L1-f1
The divergency at this place may be found out by tracing the bordering rays
and the tangent of a half divergency angle is:
alfa2 delta1 L1 alfa1
tg(-----) = ------- + ---- * tg(-----)
2 2*f1 A1 2
If the size of the source is small in comparison with the focal length of
the entrance lens (delta1<<f1) then tg(alfa2/2) = tg(alfa1/2)*L1/A1. If the
angles are small too then: alfa2=alfa1*(L1/A1): i.e. the divergency was scaled
in proportion of the ratio of the distance between the lens and the object to
the distance between the lens and the image. Having noticed that the ratio of
these spacings is equal to the ratio of the source size to the image size one
can again note that the angular magnification is in reverse to the linear one.
- In order to get the final image at the distance L2 from the output lense,
the output lense itself should be placed at a certain distance A2 from the
intermediate image given by the entrance lens. The exact value of L2 follows
again the formulae of thin lens:
f2*L2
A2 = -------
L2 - f2
With knowing the distance and divergency one can get the size of the spot at
the output lens (in other words the required diameter of the output lens):
D2 = delta2 + A2*2*tg(alfa2/2)
Lets look at the D2/D1 ratio:
D2 delta2 + A2*2*tg(alfa2/2)
-- = -------------------------
D1 delta1 + L1*2*tg(alfa1/2
To look at this Without any additional assumptions wont give us any use.
Lets take that delta1<<D1 and delta2<<D2:
D2 A2*2*tg(alfa2/2) A2*tg(alfa2/2)
-- ~~ ---------------- = --------------
D1 L1*2*tg(alfa1/2) L1*tg(alfa1/2)
And now we can use an approximation for tg(alfa2/2):
tg(alfa2/2) ~~ tg(alfa1/2)*(L1/A1), and finally:
D2 A2*tg(alfa2/2) A2*tg(alfa1/2)*(L1/A1) A2
-- ~~ -------------- ~~ ---------------------- = --
D1 L1*tg(alfa1/2) L1*tg(alfa1/2) A1
Previously, in the case of telescope tuned to the infinity, we've seen that
the size of the beam was magnified by the ratio of focal lengthes times. Now
the role of the focal lengthes ratio is played by the ratio of the distances
between the correspondent lens and the intermediate image inside the telescope.
Do note that in the process of getting this relation, there was no need to
assume that the angles (alfa1, alfa2, etc...) are small. It was enough that
the source was small in comparison with the entrance lens, and the intermediate
image was small in comparison with output lense, (Such a situation is often
when some laser diode is being focused by a telescope).
- Finally with knowing the intermediate image size delta2, with distance
from it to the output lens A2 and having the distance from the output lens to
the final image L2 we can now get the size of that final image (or the size of
the laser beam spot):
L2-f2 f1 L2-f2
delta3 = delta2*(L2/A2) = delta2* ----- = delta1*-----*------ =
f2 L1-f1 f2
f1*L1 L2-f2 L2 A1
= ----- * ----- * delta1 *(L2/L1) = -- * -- * delta1
L1-f1 f2*L2 L1 A2
I.e. the size of the final spot is related to the size of the light source
in the straight proportion to the ratio of the distances (the one from the
final image to the telescope and the one from the source to the telescope) and
in the straight proportion to the angular magnification.
For more clearance we may rewrite the relation this way:
delta3 L2 D1
------ = -- * --
delta1 L1 D2
...From where it is completely clear that the greater the diameter of the
output beam is, the smaller the final spot will be.
Additionally one might note that in our approximation D1/L1~~alfa1. So:
L2
delta3 = delta1*--*alfa1
D2
I.e. the obtainable size of spot at a given distance depends only to the
size of the source delta1, to the angular divergency alfa1, and to the
ratio of the distance L2 to the output beam size D2. In case of point-like
image The last ratio would also express the angular convergency of the beam.
Exactly the same expressions one can obtain for Galilean type telescope.
The difference would only be the virtuality of the intermediate image and
that this image is situated not completely inside the telescope but to the
left from its entrance lens.
The similar expression may be obtained for the case when a radiation from
the source is being focused by some single lensed collimator. The next picture
stows this case. Designations of distances and angles are to the most extent
correspond to the previous picture.

From the picture it is evident that delta3 = delta1*(L2/L1) and
L2 L2 L2
delta3 = delta1*-- = delta1*alfa1*-------- = delta1*--*alfa1
L1 L1*alfa1 D2
It means that if the size of the lit area on the output lense is kept
unchanged, collimator provides at the given distance the spot of the same
size as telescope does. (Evidently if the source in both cases has the same
size too).
Independently to what optical scheme You use, the parameter of the most
importance is the size of the output beam.
Conclusion: Your possibilities to focus the beam are determined only by
the diameter of optics available to You.
 Return to contents Return to contents
F. Anamorphotic prisms
↑
The interesting fact to note is that the law of light refraction (Snell's
law) for the border of two media does literally estate the inequality of the
angles of incidence and refraction. This fact immediately causes inequality
of sizes of incident and refracted beams:

The inequality of sizes of the incoming and outcoming beams is nothing else
than the linear magnification. And we know, that any linear magnification
is accompanied with angular one. Lens see if it is true.
If a ray falls on the boundary interface as it is shown on the picture above,
the angle of incidence is related with the angle of refraction by the next
expression: n2*sin(alfa2) = n1*sin(alfa1) (this expression is also called as
Snell's law).
Imagine that infinitively close to the first ray, we have a second one and
it goes at a little angle to the first one. Let's designate this little change
of angle of incidence as d_alfa1. I.e. the angle of incidence of the new ray
will be alfa1+d_alfa1. And the correspondent angle of refraction for the second
ray we will seek in the form of alfa2+d_alfa2. We are free to do so, because
d_alfa2 is to be found and it does not limit the result yet. d_alfa2 is then
the unknown (and probably small) deflection from the initial refraction angle.
The Snell's law for the new ray will look like this:
n2*sin(alfa2+d_alfa2) = n1*sin(alfa1+d_alfa1)
Let s use the school formula for the sine of the sum of angles:
sin(A+B) = sin(A)cos(B) + cos(A)sin(B).
We will get:
n2*[sin(alfa2)*cos(d_alfa2)+cos(alfa2)*sin(d_alfa2)] = n1*[sin(alfa1)*cos(d_alfa1)+cos(alfa1)*sin(d_alfa1)]
Now let's assume that d_alfa1 and d_alfa2 are small enough to consider that:
cos(d_alfa1) = 1; cos(d_alfa2) = 1;
sin(d_alfa1) = d_alfa1 ; sin(d_alfa2) = d_alfa2.
It seems like if we approximate cosines of small angles with unity, we should
approximate the sines by zeros. There's no answer for this question in the
school maths. In the course of mathematical analysis it is proven that the
approximation that a cosine of a small angle is close to unity is more precise
(has second order of vanishing) than the approximation that a sine of a small
angle is zero (has only first order of vanishing).
Making the mentioned substitutions:
n2*[sin(alfa2) + cos(alfa2)*d_alfa2] = n1*[sin(alfa1) + cos(alfa1)*d_alfa1]
Now lets subtract n2*sin(alfa2) = n1*sin(alfa1) from there.
The remaining will be: n2*cos(alfa2)*d_alfa2 = n1*cos(alfa1)*d_alfa1
If we remember that angular magnification M is just the ratio of angles:
M = d_alfa2/d_alfa1;
We will get that the angular magnification is equal to:
n1*cos(alfa1) n1 h1
M = ------------- = -- * --
n2*cos(alfa2) n2 h2
I.e. small variation of angle of incidence causes M times greater variation
in the refraction angle, and this M with the precision to the factor (n1/n2)
is reciprocal to the linear magnification.
The factor (n1/n2) reminds us that here we have a transition from one optical
medium to another. Earlier we had not meet with this because lenses were
assumed as being placed into some uniform medium. I.e. both borders of the
lense are connected to the same medium.
Here we can also note that even at normal (orthogonal) incidence of a light
beam onto the boundary interface (cos(alfa1)=cos(alfa2)=1) the angular
magnification will still be not unity but M(alfa1=0)=n1/n2.
Further considerations can show that M = tg(alfa2)/tg(alfa1), which means
that if a beam propagates from some medium with higher optical density (glass,
water, plastic) into some lesser optical dense medium, then the closer the
angle of the beam outcome to the tangent to the boundary surface, the higher
the angular magnification will become. When the incidence angle approaches
the angle of full internal refraction, the angular magnification approaches
the infinity.If we take a plano-parallel piece of glass there will be nothing interesting.

Any angular/linear magnification given by the first face will be exactly
compensated my the linear/angular diminishing given by the second face.
To observe the phenomenon and to use it in practice we will need to make
an oblique cut, i.e. to cut a prism:

By giving angular and linear magnification and by transforming one parallel
beam into another parallel beam, prism is essentially a telescope always tuned
to the infinity. The fact that this telescope is rarely used in practice can
be explained in the first place by the fact that this telescope is astigmatic
one, and astigmatic telescopes are of rare use. One may also note that prism
transforms one parallel beam into another parallel beam only if the light is
monochromatic. Otherwise the prism will give a colored spray of rays as it is
widely known. For a real telescope this would be called as "chromatic
aberration."
The principle described above is shown on the next educational video, of the kind You should have seen at school during lessons of physics:
On the other hand, the optics for laser diodes is exactly the place, where
the astigmatic properties are handy and the radiation has narrow enough
spectrum, for one to neglect the chromatic aberration.
 Return to contents Return to contents
Single prism
↑
The behaviour of a ray of light can be described by using the refraction law
twicely, The first time - for the entrance face and the second time - for the
output face of the prism. Generally the formulas are rather cumbersome and
it is not clear enough what follows from them. It is a pity, but serious
simplifications are only possible for the small number of particular cases
(like small angles of incidence and of refraction, case of equilateral prism
with the ray being parallel to its basement inside it and so on). However
we can still make a few general statements without getting into the details
of ray tracing.
If alfa1 - is the angle of incidence onto the entrance face of the prism (let
me remind that angles of incidence and refraction are counted from
the line, orthogonal to the refracting surface);
alfa2 - angle of refraction on the first face;
alfa3 - angle of incidence of the beam onto the output face;
alfa4 - angle of refraction on the output face;
M1 - angular magnification on the first face;
M2 - angular magnification on the second face;
H1 - linear magnification on the first face;
H1 - linear magnification on the second face;
n1 - refraction index of the prism's material;
n2 - refraction index of the surrounding medium;
then by repeating the above corroborations one can get:
n2*cos(alfa1) n1*cos(alfa3)
M1 = ------------- ; M2 = -------------
n1*cos(alfa2) n2*cos(alfa4)
and the full angular magnification is:
n2*cos(alfa1)*n1*cos(alfa3) cos(alfa1)*cos(alfa3) 1
M = M1*M2 = --------------------------- = --------------------- = -----
n1*cos(alfa2)*n2*cos(alfa4) cos(alfa2)*cos(alfa4) H1 H2
I.e. (n2/n1) factor has successfully canceled itself and the angular
magnification has again become reciprocal to the linear one.
However the exact value of the angular/linear magnification depends strongly
and not linearly to the angles of entrance/exit of the rays. Sometimes it is
handy: one can vary the magnification just by setting the prism to various
angles. In other cases it "suddenly" complicates the life. E.g. if one tries
to use a prism to transform a beam with large enough angle of aperture, the
output beam would be like consisting of a plurality of smaller beams and each
of these partial beams was magnified individually with different magnification
factors. The same will be observed if one tries to transform a beam with
low angular divergency into a fan-like one. These distortions are very hard
to tolerate. In some sense they are similar to "grey divergency".
Particularly this limitation does not allow to use a prism to compensate
fast axis divergency of laser diode radiation. Equally, an attempt to equalize
the fast axis divergency with slow axis one will also cause difficulties.
On the other hand prism is suitable for use with slow divergent beams.
Imagine You have a diode with internal FAC lense. Without knowing our (user's)
problems the manufacturer usually installs the FAC lens into the position of "full compensation" - i.e. in the position, where the beam has minimal possible
divergency along the fast axis. On the other side we would like it to be
equal to the divergency along the slow axis (this statement was discussed in
the subpart "collimator", see above). And here is the very place for the prism:

If one looks at the problem in the plane of (old) fast axis (as it is shown
on the picture) the image of the diode appears to be slightly moved forward
relatively to the diode itself. So for the most sharp focusing one still needs
to tilt the lens. I dont want to make You tired with formulas, allowing to
calculate the needed the correct amount of tilt. Let's say that if the prism
is installed close to the diode's output window and if the path of rays in
the prism's glass is short enough, the difference required for being
compensated by the lens tilt can be made small enough and the angles of tilt
appear to be very acceptable.
Generally the process is like that:
- We have a diode with FAC lense;
- At a distance of less than a millimeter from its output window we carefully
place a prism. Literally insert the prism's edge into the beam;
- Tilt the prism until the divergencies along both axis become equal to each
other (the laser spot should become square shaped);
- At the output of this assembly we install a lense collimator and carefully
adjust the distance to the collimator lense and its tilt (in optics the
procedure of "careful adjustment of distance and tilt" has the name "alignment".)
- Measure sizes and angles and using these data draw the casing for the
whole husbandry
 Return to contents Return to contents
Double prism
↑
In principle nothing forbids to place two, three or even more prisms in
series (along the beam path). Generally the prisms are placed arbitrary:

And each of the prisms adds its own angular and linear magnification. The
ray trace calculations here are reduced to sequential applying of Snell's
law to each boundary interface on the path of the ray. The formulas become
more and more cumbersome and their sense becomes less and less comprehendible.
Maybe one of you will find the unique combination of prisms and their
positions, that will make the humankind happy - that will be able to solve
all the problems and will have no shortcomings.
And yet, while we are still waiting for this to happen, let's discuss
an important particular case: pair of prisms. Imagine, there are two similar
prisms, having been placed as it is shown on the next picture. And assume a
beam, having been emitted from a source S, comes to the entrance face of
that pair of prisms:

Let the aperture angle of the beam along x axis is beta and the one along
y axis is alfa. Let H be linear magnification of one of the prisms. The sizes
and aperture angles of the beam in the pints of importance are shown on
the picture near the corresponding points and surrounded by frames. The
formulas are for small angles (when sin(alfa)=tg(alfa)=alfa and sin(beta)=tg(beta)=beta;
alfa and beta are measured in radians) and for the thin prisms
(the transformation of the beam during its path through the glass is not taken
into account).
From the formulas it can be seen that finally the pair of prisms keeps the
aperture angles of the beam. It is more than predictable since both prisms
compensate each other.
Another thing to note is that the pair of prisms allows to change the
aspect ratio of the beam's section. Indeed in the absence of prisms this
ratio would always be y/x = alfa/beta. The application of prisms allows to
change this to:
y (L+l)*alfa
- = --------------
x (L+l/H^2)*beta
I.e. one can change the proportions of the laser spot. One make oval to
become round or vice versa. But this is not the most interesting property
of the anamorphotic pair of prisms. In order to discover the more interesting
property look at the next picture:

This picture makes it completely obvious that if we have a beam from a
point-like source or from its (may be pure virtual) image, and if we know the
size a and aperture angle alfa of the beam in some section, then the distance L
from this section to the source (or to its image) will be expressed as L=a/alfa.
A bit earlier we've determined sizes and aperture angles of the beam that
had passed through the pair of prisms:
along x axis: L*beta + l*beta/H^2 ; beta
along y axis: (L+l)*alfa ; alfa
The straight consequence is that the distances (from the exit of prisms)
to the image will be
in xz plane: L + l/H^2
in yz plane: L + l
I.e. it appears to be possible to shift the source images in xz and yz planes
relatively to each other. It is easy enough to vary this shift - just increase
or decrease the spacing between the prisms. And in some cases the value of this
shift is easy to calculate. Indeed if the linear magnification exceeds 3 the
shift of image becomes equal to the spacing between the prisms with a tolerance
of about 10%.
Remember problem of the collimation of radiation of laser diode, where the
fast axis divergency was partially compensated by a cylindrical lens (see
subpart "collimator"). That time in order to compensate the appearing
difference of positions of source images in the plane of fast axis and in the
plane of slow axis we had to tilt the output lens. As we can see now, we could
just add a pair of prisms and by varying the spacing between the prisms we
could achieve the most sharp focusing, and thus the most high power density in
the beam spot. (Lemme remind that the power density is called "intensity".)

Another good thing here is that the prisms compensate aberrations of each
other. Remember what was said about transformation of a beam having large
aperture angle in a single prism. The pair of prisms is to most extent free
of this shortcoming, and can operate with much more divergent beams.
The sole drawback of the scheme, shown on the last picture, is too large
quantity of the optical surfaces, which causes enormous losses if there is
no high quality antireflection coating for the necessary wavelength.
A NOTE ON THE PRIORITY AND AUTHORSHIP: Do not think that I've invented all
the described above solutions. Most of them I've seen in optical systems
being sold. I have neither intention nor possibilities to dig through the
thousands of tons of papers in special journals for just to find out who
and when has discovered them. Some of them may be classic (belong to the
general knowledge and present in textbooks for students), others may be
covered by patents. I have no intention to offend anybody's copyright.
I just explain to You how these solutions work.
If anybody is kind enough to give me information about who invented these
things, I'll be glad to insert this information to this text.
 Return to contents Return to contents
METHODS OF POWER INCREASEMENT BY ADDING MORE LASER BEAMS TOGETHER
↑
Geometrical addition of beams
↑
The divergency of the beam of a separate laser diode is often suitable for
most application. Remember laser pointers, for example. However the power
of single diode is often less than acceptable. The straightforward way to
increase the power is to take several laser pointer and wrap them tightly into
one bunch with some duct tape. If those laser pointers are good and all the
rays from this bunch are going almost parallel to each other, then it takes
only to cover the resulting beam with a lens and all the rays will have their
focal spots close to one another. Like it was done there.
Its a pity but this approach has several failures. To be exact the sole
failure is only the low brightness when being averaged over the whole bunch of
rays. But it is simpler to explain on several examples:
First: If You need to focus the beam, it will eventually occur that the
intensity is still too low for You. E.g. laser saws wood successfully, but
You want to saw steel. You will need to make a smaller spot and it will take
You to have a lens with shorter focal lens. But we know, that a lens with
short focal lens just can not have a large diameter, So by taking smaller and
smaller lens with shorter and shorter focal length You will eventually loose
some rays, as at the picture below:

Another example is drilling. If the beam. If the beam converges rapidly after
the lens and then diverges rapidly after its narrowest place (after its neck),
You won't be able to drill a through hole in a thick material. And in reverse:
if the beam is narrow and converges slowly, it has a long neck, that allows
to drill and cut thick materials, as it is shown on the picture below:

The third example. Imagine, You want to send the laser beam far far away
and to have the spot there as small as possible. In this situation You
definitely are to expand the beam by some telescope. (Remember, how a
telescope work: "if the beam diameter was increased by k times, its
divergency becomes k times lower".) But if the beam is already wide,
it is hard to make it even wider. If we take, say, a beam, having 5 cm
diameter (like here) and if we try
to expand it, say, 5 times, we will end up with 250 mm lens. And it is
comparatively large one, almost like professional astronomy instrument.
It costs high too.
The said, i think, is enough to understand that it is bad to have a large
spacing between the separate rays of the separate diodes. But even if we
placed the diodes into close connection with one another we will still
have low effect - the bodies of the diodes, the lens mounts and etc will
become the obstacle to get a most compact beam. The ideal case would be
if we could place the rays "one inside another", without occupying any
additional place. However it is not always possible to do so. The partial
solution of the problem is given by geometrical addition, where the rays
are placed not "one inside another", but "one as close to another as possible".
One of the possible schemes of the geometrical addition is shown on the next
picture:

The mirrors are intentionally shown as being bigger than the rays sections.
One should note that it is not necessary to have too little mirrors in order
to construct this scheme.
The picture makes clear, that if the edge of each of the mirrors is straight,
and if there is no gap between the edge and the end of reflective coating, the
spacing between the separate rays can be made very small. The united beam will
be almost continuous.
It is clear that for the united beam have small divergency, the separate
rays must be as parallel to each other as possible. So the mirrors are to be
installed precisely. Worse than that, if the position and direction of laser
diodes has some scatter, it means that the installation angle must be
individual for each mirrors. In its own turn it means that the mirrors have to
be alignable, or there have to be a possibility to align them during the
installation (gluing up).
Fortunately it is not too hard to provide this. One can use a simple tool.
Its photo and cinematic scheme are shown on the pictures below:


An essence of the cinematic scheme of the device is that the axes of revolution
of the mirror pass through the center of the mirror. And the alignment screws
and bars were placed in such a way, that they do not interfere with the process
of gluing up.
It is robust to use a match as a mirror keeping handle. After the mirror
have been glued up, one can easily cut the keeping handle by some laser.
This way You can avoid mechanical stress, that can ruin the alignment. Don't
use bamboo sticks from mats. Unlike matches they are not paraffined and
use to bend and twist when the ambient temperature and humidity change,
Generally the technology it the next:
- First of all glue up the first mirror. Its up to You whether to use
the special tool or not at this stage. It does only matter that the
ray was directed in some proper direction and did not touch anything
on its way. Only the first diode must be turned on at this stage.
- Give the glue a time to cure completely. If You are using the tool,
cut off the mirror keeping handle.
- Take a new mirror and glue it to a new keeping handle (to a match) and
install the keeping handle into the tool.
- Now You need to set the mirror into proper position. Since the boom of
the tool is not movable, the only way to do this is to move the platform
where Your diodes are installed (the heatsink with the diodes, if You
want)on the tool basement under the boom. Find the position, when the
ray of the second diode hits near the end of the second mirror as it was
shown on a picture above (the enumeration of the diodes and mirrors is
from left to right). Keep an eye for the (second) mirror not to become
an obstacle for the first beam. The fist and second diodes are to be
turned on now. It is also good to keep the angle between the first and
the second rays in reasonable limits, or else the alignment range of
the tool may be just not enough to align the rays.
When the proper position of the platform with the diodes have been found,
glue it up to the basement of the tool with several drops of a hot glue
(aka glue-gun or low molecular weight polyethylene). This attachment
is to be removed later, so don't be too zealous when gluing.
- Align the ray of the second diode to the ray of the first one. Add some
glue to fixate the second mirror and leave it aside to cure up.
Dependently to the type of the glue it may take from several hours to
several days. I can not recommend to use the glues, that take more than
one day for the complete curing. Otherwise the weather (the ambient
pressure, temperature and humidity) may drift far enough to cause problems
with the alignment, even if the work is being made indoors.
- When the glue has cured, check the correctness of the alignment (by
turning on the first and the second diodes). Then cut off the mirror
keeping handle. It is better to cut without applying any mechanical
stress - for example by means of some laser pointer, rated to 1-2 W.
After the keeping handle have been cut, it has a sense to check again
if the alignment is still proper. If yes - proceed to the further step.
If not - it is a good time to remove the mirror (while the strength of the
glue has not built up) and return to the step 3. The first mirror may
be kept untouched.
- Detach the platform with the diodes from the tool's basement. (Obviously
the position of the platform relatively to the boom of the tool in any
case must be changed for the next mirror installation. Such a simple tool
allows to install only one mirror at a time.)
- Take new mirror and attach it to new keeping handle. Install the keeping
handle to the tool.
- As You did it in step 4, find a position, when the ray of the third diode
hits mirror near its edge, and when the mirror does not make an obstacle
to the pass of the beam of the second diode. The second and the third
diodes are to be turned on here. When the proper position was found, glue
the platform with the diodes to the basement of the tool.
- Attention here! At the fifth step You were aligning the ray of the second
diode to the ray of the first diode. You may propose, that now You are
to align the ray of the third diode to the ray of the first one. It is
not correct. Due to the alignment errors it is better to align the
ray of the third diode (and all the next diodes) to the ray of the first
one. Evidently the first and third diodes are to be turned on now.
Fix the position and rotation of the third mirror by the glue and let
it to cure. One may (and should) turn the diodes off for the drying period
of time.
- When the glue has cured completely, check the alignment (by turning on
the first and the third diode). Cut off the mirror keeping handle and
check the alignment again. If the alignment is improper, detach the
third mirror and repeat its installation from the very beginning (from
the step 7). One may leave the first and second mirrors untouched.
- If You are satisfied with the alignment, repeat the procedure for all the
following diodes and mirrors. You should already be familiar with it.
The result can be seen on the following photos and videos:
- The photo of a half of NUBM08 diode bank having been collimated by mirrors
and installed onto a heatsink.



- The photo of a laser beam spot in the far field (at a distance of 5 meters):

- The video of the laser beam cutting wood and metal:
With using a 50 mm focal length lens I succeeded to drill a hole in a
razor blade and the dimensions of the hole were: 0.7 mm x 0.2 mm. The whole
beam comes through this hole, it can be detected by the fact that the razor
blade quits to heat up after the hole is complete. So the focal spot has
its sizes less then those 0.7 mm x 0.2 mm. When the output power is 15 W
it gives intensity I = 15 W / (0.07 cm x 0.02 cm) = 10.7 kW/sq.cm.
Several notes at the end of this part:
- Epoxy resins are robust glues for gluing up the mirrors. There exist
resins that can cure in 3-5 minutes. However in reality this is not
curing but rather "capture". Actually the speed of the real curing
for the most of the "fast" epoxy resins is lower than the one for
the normal "slow" resins.
Additionally it is hard to apply a photo curing resin here, since it
tends to cure up under the radiation of the diode being aligned.
Before use a resin from a given tube, it is recommended to make a test
mix - to see how long it will take to cure, and how hard it will become
at the end. The experience shows, that the scatter of these parameters
from tube to tube may vary more than from one type of epoxy to another.
- The final result of the addition of the rays may be better if one makes
the "anticipating" alignment - with taking into account the predicted
drift of the alignment for the time of the epoxy curing. The drift of
the alignment is usually not due to the shrinkage of the resin (that
is the first one thinks about), but due to the instability of the alignment
tool itself. Having got some experience You will know the direction
and amount of the alignment drift dependently to the time of drift and to
the history - to the magnitude and direction of motions, having been
done during the alignment. With this knowledge You will be able to find
such position and rotation of the mirror, that will end up to the proper
position and rotation to the moment of glue curing.
- The alignment is better to be made not at the full power of the diodes
but at some smaller one. It will provide more safety to the diodes and
prevent overheat of mirrors, which is detrimental when the glue has not
yet build up its hardness.
- Note that the description above is a framework only, for not to sink in
details like each switch position and each motion. Particularly it's up
to You to decide what diodes are to be turned on and of and when. Remember
only that You should wear protective glasses even if only one diode is
powered up and even if the power has been reduced.
- If the fast axis is orthogonal to the plane of the platform containing
the diodes there appears an interesting case, see the picture below:

(The fast axis is orthogonal to the plane of the picture.)
The ray of a laser diode diverges rapidly along the fast axis until it hits
the correspondent lens. Then the ray becomes more or less parallel, but its
section becomes oval, so all the spots of the diodes on their mirrors are
elongated in the direction orthogonal to the picture plane. It means, that
one can place the rays even more tightly, than it could be if the spots were
round. Particularly the collective beam of the mentioned above 4 pcs NUBM08
diodes has 6x3 mm section at the beginning, so the intensity is equal to
83 W/sq. cm. without any kind of focusing.
 Return to contents Return to contents
Polarization summation
↑
In addition to power, divergency and color (wavelength) a beam can be
characterized by its polarization. A sole photon (as they say in quantum
mechanics) can have only one of two possible polarization states: twisted
clockwise or twisted counter clockwise if one looks towards the photon
motion direction. (The "twisted" state means that electric force field
vector behaves like being in rotational motion around the direction of
the photon's flight. A picture, illustrating this process can be found
almost in any modern textbook on optics or either in any encyclopedia.)
If a beam consists of photons of only one sort, the beam becomes
circularly polarized. And the number of different possible circular
polarization is equal to the number of different possible photon states.
To be exact there is clockwise circular polarization and counter clockwise
one.
A pair of photons having the same wavelength, but "twisted" into opposite
directions form a field, where the rotational motion of electric force
vector is compensated and the oscillations of the vector become planar.
Dependently to the phase shift between the taken photons, the orientation
of this plane of oscillations may be arbitrary. When a beam of light
consists of such photon pairs it becomes plane polarized. And if the
rotation of electric force vector is not fully compensated, the beam
appears to be elliptically polarized.
And finally if a beam consists of randomly polarized and randomly phased
photons we can call it as "non polarized" or "natural" light. Here one can
note that if all the photons have exactly the same wavelength the phase
shift between any of them is constant and thus we can sum all the electric
vectors and get the resulting polarization. This fact can be observed in
practice: totally coherent light does always have certain polarization.
On the other side we have a little chance to meet the fully coherent light
in practice.
Practically we usually deal with nonpolarized light or with light with
prevailing planar polarization. Circular and elliptic polarizations are
more exotic.
To reflect or refract light one has to use a substance. And so it comes
out, that refractive and reflective properties of substances depend to
the relation between the direction of polarization and directions that label
the substance structure and the geometry of the problem. The latter may
be: crystallographic axes, orientation of the boundary between different
substances, direction of mechanical or electrical tension and so on...
A property of the light to refract/reflect differently in dependence to
its polarization does open new approaches to the task, being insoluble in
the optics of unpolarized light: namely how to make two different beams
to have the same position and direction. I.e. how to make two beams to
be one.
The literally reverse task is solved by an optical element, being called as "polarizer". From the our task's point of view there are two main classes
of them: absorbing polarizers and dividing polarizers. The first ones transmit
light with certain polarization and absorb all other (or reversely: absorb
certain polarization and transmit anything else). The second ones split
the light into two beams with different polarization states.
Most polarizers, we meet in everyday life, are of absorptive type. These are:
stereo glasses for 3D cinema, polarizing filters for photo and video cameras,
filters for car headlights and glasses of LCD displays. Its a pity, but they
are all useless for beam combining.
Dividing type polarizers are particularly: stack of glasses, prisms of Glan,
Nicol and Volastone, and the "interference" polarizer, being essentially the
same as stack of glasses, but having very thin layers.
Even a sole glass plate represents a weak polarizer if placed at an angle to
the light beam direction. The formulas, describing the dependencies of
reflection ratios for different polarizations to the incidence angle are a bit
complicated, so we better use a graph for qualitative insight (cited from
Wikipedia, article "Fresnel equations"):

The picture represents dependencies of reflection ratios for rays having
different polarizations, coming from air into an optically dense medium
(diamond). The horizontal axis of the graph corresponds to angle of incidence.
The coefficient, designated as Rp, is for the ray being polarized in the plane
of incidence (the plane containing the ray itself and a vector, orthogonal to
the boundary of the media.) The Rs coefficient is for a ray, being polarized
orthogonally to the polarization of the first ray.
The numbers on the graph are of low interest for us (in the reality we rarely
deal with diamond). More important is the fact, that Rp coefficient has the
property to go to zero at a certain angle of incidence. That "enchanting"
angle of incidence has the name "Brewster angle" and its numeric value is
individual for any dielectric. It is equal to arctg(n2/n1), where n1 - is
the refraction index of the medium, where the ray is coming from, and n2 -
is the reflection index of the medium, where the ray gets into. For the glass
in air (n2=1.5 n1=1) the Brewster angle is 56 degrees. For glass in water
(n2=1.5 n1=1.3) the Brewster angle is 49 degrees.
It is clear, that if we take a glass plate and place it at the Brewster
angle to some beam of light, the reflected part of the beam would be fully
polarized. However the same can not be said about the part, that have passed
the plate. The "unwanted" polarization will only be slightly reduced in the
transmitted light, because the corresponding reflection coefficient is
small. The similar situation would take place if we try to combine two beams
using a sole glass plate. The beam polarized in the plane of incidence will
pass by without losses, but only a little part of the second beam will be
added:

To increase the reflection, one could try to stack several plates and place
this stack at the Brewster angle to the beam. However the quality of passed and
reflected beams will be bad in this case:

On the other hand, the thinner the plates, the higher is the quality. As the
limit of the design we have a thin film dielectric polarizer (of interference type).
The pictures above make clear the principle of polarization beam combining:
one needs to take a dividing type polarizer and invert the problem of its
common use. Commonly the polarizer divides a beam of unpolarized light into
two ones, each coming in its own direction. For the polarization combining, we,
in reverse, take two lasers, orient them to have their polarizations to be the
same as the resulting beams in the common problem had, and direct the laser
rays along the ways of the resulting beams in the common problem. At the
opposite side of the polarizer there appears a beam, having the power equal
to the sum of the incoming beams powers, excluding maybe the optical losses.
It is clear, that a precise alignment is needed in order for the beams to
become highly coincident in their direction and position.
However the alignment is not the prime difficulty. Two other conditions:
one must have two lasers, emitting polarized light, and the polarizer of
dividing type. The first condition is easy to be met. Most lasers tend to
emit polarized light even if no efforts have been applied to achieve this. The
polarization degree of many common commercial laser diodes is about 90%.
The other condition can cause severe problems.
While absorptive polarizers have extensive home use, the dividing type
polarizers are almost impossible to find at home. Some polarization prism
(Nicol, Glan or Volastone) can be scavenged from an old exotic optical
instrument if You've got a proper one. Being new, those prisms are highly
expensive. Interference (thin film fully dielectric) polarizers are much
cheaper, but they work properly only in narrow part of spectrum near
their design wavelength. And to make things more sorrow, the polarizers
of this kind with the design wavelength of interest (808 nm, 975 nm,
450 nm and 520 nm) are ridiculously hard to find.
Almost sole solution - is to acquire so called "PBS cube" on eb@y.
PBS stays for "polarizing beam splitter". The next three photos and short
video demonstrate how a PBS cube reacts on the laser pointer rotation.



One can see that rotation of the laser pointer affects the beam behaviour
strongly. At the beginning the most of laser power comes straightly through
the prism without sufficient losses. At 45 degrees the incident power is
divided almost equally between the passing and reflected beams. And finally
at 90 degrees almost the whole beam is reflected by the prism. The straight
coming power is at minimum.
The polarization beam combining seems attractive at the first glance:
one can double the power of beam without changing its size and divergency.
However the things are not so good in the laser diodes reality. The
specialties of laser diode as the source of light (the shape of its light
emitting body and its highly non uniform divergency) do nullify the advantages
of the polarization beam combining to the most extent.
Indeed if we take two diodes, place them as shown on the picture

and if we combine their beams using PBS cube we will see that the far field
pattern of the beam becomes cross shaped. The cross is formed by two stripes
of light formed by each of the diodes.
I.e. if the beam of one diode diverges strongly along one axis and diverges
slowly along another, then the combined beam will diverge fast along both of
the axes. And the intensity of the light will be doubled only in the area,
where both stripes overlap each other. The intensity of the rest part of the
beam will be unchanged. In fact if we had a mirror with a little slit in
its center (see the figure below) we could create a system of geometrical
combining with almost the same results, excluding maybe, little loss of
the radiation in the area of overlapping of the stripes:

 Return to contents Return to contents
Spectral Combining
↑
Not only the beams with different polarization can be combined into one
beam. One can do the same with beams that have different wavelengthes. Let's
remember the principle of operation of any spectral gauge (like spectrograph,
monochromator and so on): there exists a special optical element (like prism
or diffraction grating) that can disperse the beam of white light into a
fan of colored rays coming at different angles. One should be able to
understand that the problem can be inversed: if we have a number of rays with
different colors, we could specially choose their position and direction of
incidence onto the dispersive element, for the latter to combine them into
one beam. Not necessary that the combined beam will have white color. It
depends strongly to the balance of powers in the rays of different colors
being combined. However the total power in the combined beam will be the
sum of powers of the combined beamlets without maybe some losses.
In practice for the spectral combining it is more robust to use a so called
"dichroic mirror", i.e. a mirror, that reflects well a light with one
wavelength and transmits well a light with another wavelength. These mirrors
are much more affordable than You might thought. In fact, most of laser
mirrors, mirrors from DVD-drives, mirrors from light stage machines are
dichroic ones. For example a He-Ne laser mirror reflects well red light and
transmits well blue and green colors. A mirror from a DVD-drive head has
similar properties, but its maximum of reflectance is shifted towards deeper
red color. One can also find a "beam combiner cube" in internet shops. It
is used widely for synthesis of beams with arbitrary colors.

The principle of beam combining using a dichroic mirror is illustrated on
the next picture:

One can note that the geometry of the problem is even more simple than for
the case of polarization combining. Generally the effectiveness of the
combining keeps certain dependency to the rotation of lasers - because the
coefficients of the reflection still depend to the polarization state. But
in this problem this dependency is not the determining one.
If You want to combine red and blue beams there should not be serious
troubles with acquiring a suitable mirror. At the least case one could use
a DVD-drive mirror.

It's worse if You have to combine beams of other colors (e.g. blue with green,
blue with violet, etc...). Mirrors, suitable for those tasks, are very hard to
find. So if You have no access to mirror sputtering machine, You last resort
will probably be to use a prism or diffraction grating (as it was mentioned at
the beginning of this part). However the absence of suitable mirror is not the
main drawback of the method. Worse is that actually there is almost nothing to
combine. Indeed, as it was mentioned above, among the (comparatively)
affordable diodes only the infrared (~975 nm & ~808 nm) and blue (~450nm) ones
do exceed 1 Wt power rating. And it is almost senseless to add 0.5-1 Wt of
power to some beam of five Watts. The addition may even not exceed the losses.
So maybe the sole variant of interest is to combine beams of blue 5Wt rated
diode and IR 5Wt rated one
<< HOME PAGE |



